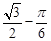题目内容
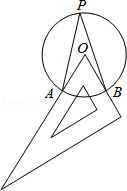
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC .
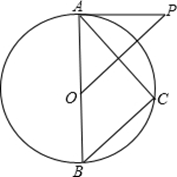
(1)求证:PA为⊙O 的切线;
(2)若OB=5,OP=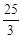 ,求AC的长.
,求AC的长.

(1)求证:PA为⊙O 的切线;
(2)若OB=5,OP=
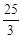 ,求AC的长.
,求AC的长.解:(1)证明:∵AB是⊙O的直径,∴∠ACB=900。
∵OP∥BC,∴∠B=∠AOP。
又∠P=∠BAC ,∴△ABC∽△POA,∴∠PAO=∠ACB=900。
∴PA为⊙O 的切线。
(2)∵OB=5,AB是⊙O的直径,∴OA=5,AB=2OB=10。
由(1)知,△ABC∽△POA,∴ 。
。
又∵OP=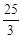 ,∴
,∴ 。
。
在Rt△ACB中, 。
。
∴AC的长为8。
∵OP∥BC,∴∠B=∠AOP。
又∠P=∠BAC ,∴△ABC∽△POA,∴∠PAO=∠ACB=900。
∴PA为⊙O 的切线。
(2)∵OB=5,AB是⊙O的直径,∴OA=5,AB=2OB=10。
由(1)知,△ABC∽△POA,∴
 。
。又∵OP=
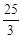 ,∴
,∴ 。
。在Rt△ACB中,
 。
。∴AC的长为8。
(1)要证PA为⊙O 的切线只要证∠PAO =900,通过直径所对圆周角是直角可得∠ACB=900,从而由△ABC∽△POA即可得证。
(2)同(1)△ABC∽△POA,利用相似比求得BC的长即可由勾股定理求得AC的长。
(2)同(1)△ABC∽△POA,利用相似比求得BC的长即可由勾股定理求得AC的长。

练习册系列答案
相关题目
 ,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为 .
,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为 .

 )。
)。