题目内容
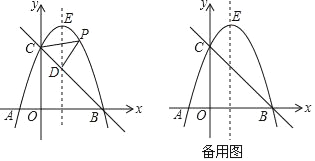
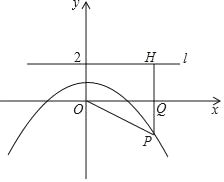
【题目】如图,P(m,n)是抛物线y=﹣![]() +1上任意一点,l是过点(0,2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H,PH交x轴于Q.
+1上任意一点,l是过点(0,2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H,PH交x轴于Q.
(1)(探究)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= .
(2)(证明)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
(3)(应用)当OP=OH,且m≠0时,求P点的坐标.
【答案】(1)1,1,5,5;(2)OP=PH;(3)P(2![]() ,﹣2)或(﹣2
,﹣2)或(﹣2![]() ,﹣2).
,﹣2).
【解析】
(1)根据勾股定理,可得OP的长,根据点到直线的距离,可得可得PH的长;
(2)根据图象上的点满足函数解析式,可得点的坐标,根据勾股定理,可得PO的长,根据点到直线的距离,可得PH的长;
(3)当OP=OH,且m≠0时,由(2)可知△OPH是等边三角形,进而求得∠HOQ=30°,解直角三角形即可求得.
解:(1)当m=0时,P(0,1),OP=1,PH=2﹣1=1;
当m=4时,y=﹣3,P(4,﹣3),OP=![]() =5,PH=2﹣(﹣3)=5,
=5,PH=2﹣(﹣3)=5,
故答案为:1,1,5,5;
(2)猜想:OP=PH,
证明:PH交x轴与点Q,
∵P在y=﹣![]() x2+1上,
x2+1上,
∴设P(m,﹣![]() m2+1),PQ=|﹣
m2+1),PQ=|﹣![]() x2+1|,OQ=|m|,
x2+1|,OQ=|m|,
∵△OPQ是直角三角形,
∴OP=![]() =
=![]() =
=![]() =
=![]() m2+1,
m2+1,
PH=2﹣yp=2+![]() m2﹣1=
m2﹣1=![]() m2+1
m2+1
OP=PH.
(3)∵OP=PH,
∴当OP=OH,三角形OPH是等边三角形,
∵OQ⊥PH,
∴∠HOQ=30°,
∴OQ=![]() HQ=2
HQ=2![]() ,
,
∴P点的横坐标为±2![]() ,
,
∴P(2![]() ,﹣2)或(﹣2
,﹣2)或(﹣2![]() ,﹣2).
,﹣2).

练习册系列答案
相关题目