题目内容
【题目】如图1矩形ABCD中,点E是CD边上的动点(点E不与点C,D重合),连接AE,过点A作AF⊥AE交CB延长线于点F,连接EF,点G为EF的中点,连接BG.
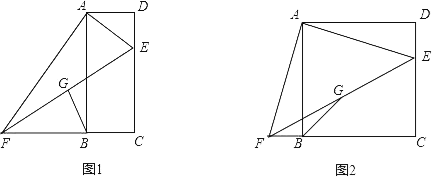
(1)求证:△ADE∽△ABF;
(2)若AB=20,AD=10,设DE=x,点G到直线BC的距离为y.
①求y与x的函数关系式;②当![]() 时,x的值为 ;
时,x的值为 ;
(3)如图2,若AB=BC,设四边形ABCD的面积为S,四边形BCEG的面积为S1,当![]() 时,DE:DC的值为 .
时,DE:DC的值为 .
【答案】(1)见解析;(2)①![]() ,②
,②![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据两角对应相等的两个三角形相似即可证明.
(2)①如图1中,作GH⊥BF于H.利用三角形的中位线定理,推出EC=2y,再根据DE+EC=20,即可解决问题.
②由![]() ,可以假设EC=24k,BG=13k,利用相似三角形的性质构建方程求出k即可解决问题.
,可以假设EC=24k,BG=13k,利用相似三角形的性质构建方程求出k即可解决问题.
(3)如图2中,连接BE,设DE=a,CD=BC=b.构建一元二次方程,即可解决问题.
解:(1)证明:如图1中,
∵AE⊥AF,
∴∠EAF=90°,
∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠ABF=∠D=90°,
∴∠EAF=∠BAD,
∴∠FAB=∠DAE,
∵∠ABF=∠D=90°,
∴△ADE∽△ABF.
(2)①如图1中,作GH⊥BF于H.
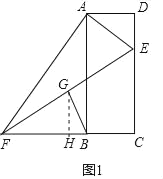
∵∠GHF=∠C=90°,
∴GH∥EC,
∵FG=GE,
∴FH=HC,
∴EC=2GH=2y,
∵DE+EC=CD=AB=20,
∴x+2y=20,
∴y=﹣![]() x+10(0<x<20).
x+10(0<x<20).
②∵![]() ,
,
∴可以假设EC=24k,BG=13k,
∵EC=2GH,
∴GH=12k,
∴![]()
∴FH=CH=5k+10,
∴FB=10k+10,
∵![]()
∴x=20﹣24k,
∵△ADE∽△ABF,
∴![]()
∴![]()
∴k=![]()
∴x=![]()
故答案为:![]()
(3)如图2中,连接BE,设DE=a,CD=BC=b.
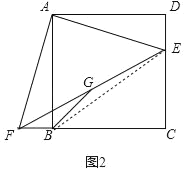
易证△ADE≌△ABF,可得BF=DE=a,
∴![]()
∵S=b2,S=4S1,
∴b2=2b2﹣a2﹣ab,
∴a2+ab﹣b2=0,
∴![]()
∴![]() 或
或![]() (舍弃),
(舍弃),
∴![]()
故答案为:![]()