题目内容
【题目】已知抛物线y=﹣![]() ﹣15有最高点(0,1),过点C(0,2)的直线l平行于x轴,O为坐标原点.
﹣15有最高点(0,1),过点C(0,2)的直线l平行于x轴,O为坐标原点.
(1)求m的值;
(2)求证:该抛物线上的任意一点到原点O的距离都等于这个点到直线l的距离;
(3)若点P,Q是抛物线上的任意两点,且PQ=9,点G是线段PQ的中点,求点G到直线l距离的最小值.
【答案】(1)m=4;(2)见解析;(3)4.5
【解析】
(1)由抛物线的顶点坐标为(0,1),可得m的值;
(2)设抛物线上的任意一点M(![]() ),则OM=
),则OM=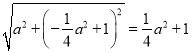 ,过点M作MN⊥l于N,可得MN=
,过点M作MN⊥l于N,可得MN=![]() =OM,则结论得证;
=OM,则结论得证;
(3)过点Q作QA⊥l于A,过点P作PB⊥l于B交l′于D,取DQ中点E,连接GE并延长交l于F,可得GF=![]() (AQ+BP),则GF=
(AQ+BP),则GF=![]() (OQ+OP),当点O,P,Q在同一直线上时,OQ+OP最小,求出点G到直线l距离的最小值为4.5.
(OQ+OP),当点O,P,Q在同一直线上时,OQ+OP最小,求出点G到直线l距离的最小值为4.5.
(1)∵抛物线的最高点为(0,1),
∴![]() ,
,
解得:m=4;
(2)由(1)得抛物线的解析式为![]() ,
,
设抛物线上的任意一点M(![]() ),
),
则OM=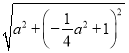
=![]()
=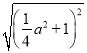
=![]() ,
,
过点M作MN⊥l于N,则MN=![]() =OM,
=OM,
∴抛物线上的任意一点到原点O的距离都等于这个点到直线l的距离;
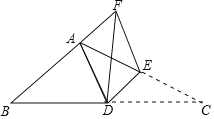
(3)将直线l向下平移,使其经过点Q,设平移后的直线为l′,
如图,过点Q作QA⊥l于A,过点P作PB⊥l于B交l′于D,取DQ中点E,连接GE并延长交l于F,
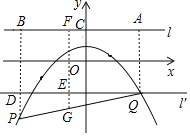
∵EG是△QDP的中位线,
∴GE∥DP,且EG=![]() ,
,
∴GE⊥l′,
易证:EF=AQ=BD,
∴GF=EF+EG=![]() (AQ+BD+DP),
(AQ+BD+DP),
=![]() (AQ+BP),
(AQ+BP),
由(2)得:AQ=OQ,BP=OP
∴GF=![]() (OQ+OP),
(OQ+OP),
∵当点O,P,Q在同一直线上时,OQ+OP最小,且最小值等于PQ=9,
∴![]() ,
,
∴点G到直线l距离的最小值为4.5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目