题目内容
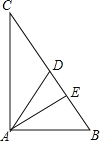
【题目】如图,Rt△ABC中,∠A=90°,AD、AE分别是BC边的中线和高,若cosB=![]() ,BC=10.
,BC=10.
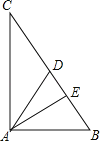
(1)求AB的长;
(2)求AE的长;
(3)求sin∠ADB的值.
【答案】(1)6;(2)![]() ;(3)
;(3)![]()
【解析】
(1)在Rt△ABC中,通过解直角三角形可求出AB的长;
(2)在Rt△ABC中,利用勾股定理可求出AC的长,再利用面积法可求出AE的长;
(3)利用直角三角形斜边上的中线等于斜边的一半可求出AD的长,在Rt△AED中,利用正弦的定义可求出sin∠ADB的值.
解:(1)在Rt△ABC中,∠A=90°,cosB=![]() ,BC=10,
,BC=10,
∴AB=BCcosB=10×![]() =6.
=6.
(2)在Rt△ABC中,∠A=90°,BC=10,AB=6,
∴AC=![]() =
=![]() =8.
=8.
∵AE是BC边的高,
∴![]() ACAB=
ACAB=![]() BCAE,即
BCAE,即![]() ×8×6=
×8×6=![]() ×10AE,
×10AE,
∴AE=![]() .
.
(3)Rt△ABC中,AD是BC边的中线,BC=10,
∴AD=![]() BC=5.
BC=5.
在Rt△AED中,∠AED=90°,AD=5,AE=![]() ,
,
∴sin∠ADB=![]() =
=![]() =
=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目