题目内容
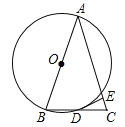
【题目】已知:如图:△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O. 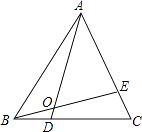
(1)求证:△ACD≌△BAE;
(2)求∠AOB的度数.
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,BC=AC,
∵BD=CE,
∴BC﹣BD=AC﹣CE,
∴AE=CD,
在△ACD和△BAE中

∴△ACD≌△BAE(SAS)
(2)解:∵△ACD≌△BAE,
∴∠CAD=∠ABE,
∴∠AOE=∠BAD+∠ABE=∠BAD+∠CAD=∠BAC=60°,
∴∠AOB=180°﹣60°=120°
【解析】(1)根据等边三角形的性质求出∠BAC=∠C=60°,AC=BC,求出AE=CD,根据SAS推出全等即可;(2)根据全等三角形的性质求出∠CAD=∠ABE,根据三角形外角性质求出∠AOE=∠BAC=60°,即可得出答案.
【考点精析】通过灵活运用三角形的外角和等边三角形的性质,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等边三角形的三个角都相等并且每个角都是60°即可以解答此题.

练习册系列答案
相关题目