ÌâÄżÄÚÈĘ
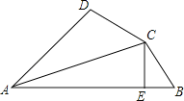
ĄŸÌâÄżĄżŁšÎÊÌⱳŸ°Ł©ÈçÍŒ1ËùÊŸŁŹÔÚ![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ”ăDÎȘÖ±Ïß
ŁŹ”ăDÎȘÖ±Ïß![]() ÉϔĞö¶Ż”㣚ȻÓëBĄąCÖŰșÏŁ©ŁŹÁŹœá
ÉϔĞö¶Ż”㣚ȻÓëBĄąCÖŰșÏŁ©ŁŹÁŹœá![]() ŁŹœ«Ï߶Î
ŁŹœ«Ï߶Î![]() ÈÆ”ăD°ŽËłÊ±Őë·œÏòĐęŚȘ90ĄăŁŹÊč”ăAĐęŚȘ”œ”ăEŁŹÁŹœá
ÈÆ”ăD°ŽËłÊ±Őë·œÏòĐęŚȘ90ĄăŁŹÊč”ăAĐęŚȘ”œ”ăEŁŹÁŹœá![]() .
.
ŁšÎÊÌâłőÌœŁ©Èçčû”ăDÔÚÏ߶Î![]() ÉÏÔ˶ŻŁŹÍščęčÛČìĄąœ»ÁśŁŹĐĄĂśĐÎłÉÁËÒÔÏ”ĜâÌâˌ·Łșčę”ăEŚś
ÉÏÔ˶ŻŁŹÍščęčÛČìĄąœ»ÁśŁŹĐĄĂśĐÎłÉÁËÒÔÏ”ĜâÌâˌ·Łșčę”ăEŚś![]() œ»Ö±Ïß
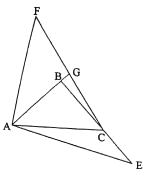
œ»Ö±Ïß![]() ÓÚFŁŹÈçÍŒ2ËùÊŸŁŹÍščęրÜ
ÓÚFŁŹÈçÍŒ2ËùÊŸŁŹÍščęրÜ![]() ______ŁŹżÉÍÆÖ€
______ŁŹżÉÍÆÖ€![]() ÊÇ_____ÈęœÇĐÎŁŹŽÓ¶űÇó”Ă
ÊÇ_____ÈęœÇĐÎŁŹŽÓ¶űÇó”Ă![]() ______Ąă.
______Ąă.
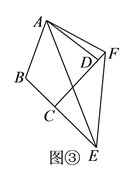
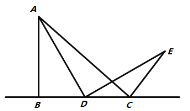
ŁšŒÌĐűÌœŸżŁ©Èçčû”ăDÔÚÏ߶Î![]() ”ÄŃÓł€ÏßÉÏÔ˶ŻŁŹÈçÍŒ3ËùÊŸŁŹÇółö
”ÄŃÓł€ÏßÉÏÔ˶ŻŁŹÈçÍŒ3ËùÊŸŁŹÇółö![]() ”ĶÈÊę.
”ĶÈÊę.
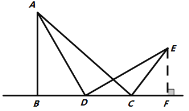
ŁšÍŰŐčŃÓÉìŁ©ÁŹœÓ![]() ŁŹ”±”ăDÔÚÖ±Ïß
ŁŹ”±”ăDÔÚÖ±Ïß![]() ÉÏÔ˶ŻÊ±ŁŹÈô
ÉÏÔ˶ŻÊ±ŁŹÈô![]() ŁŹÇëÖ±œÓĐŽłö
ŁŹÇëÖ±œÓĐŽłö![]() ”ÄŚîĐĄÖ”.
”ÄŚîĐĄÖ”.
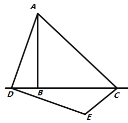
͌1 ͌2 ͌3
ĄŸŽđ°žĄżŁš1Ł©ĄśADBŁŹ”ÈŃüÖ±œÇŁŹ135ĄăŁ»Łš2Ł©45ĄăŁ»Łš3Ł©![]() .
.
ĄŸœâÎöĄż
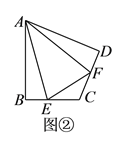
Łš1Ł©ÎÊÌâłőÌœŁșÓÉĐęŚȘ”ÄĐÔÖÊ”Ă”œĄÏADE=90ĄăŁŹAD=DEŁŹÔòĄÏADB+ĄÏEDF=ĄÏADB+ĄÏDAB=90ĄăŁŹ”Ă”œĄÏDAB=ĄÏEDFŁŹÔòžùŸĘAAS”Ă”œĄśDEFĄŐĄśADBŁ»ÔòEF=BDŁŹDF=ABŁŹÔòAB=AC=DFŁŹ”Ă”œBD=CF=EFŁŹÔòĄśCEFÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁ»ŽÓ¶ű”Ă”œĄÏDCE=135ĄăŁ»
Łš2Ł©ŒÌĐűÌœŸżŁșčę”ăEŚśEGĄÍCDŁŹÓ룚1Ł©ÍŹÀíŁŹżÉÖ€ĄśABDĄŐĄśDGEŁŹ”Ă”œBD=GEŁŹAB=DG=BCŁŹÔòBD=CG=GEŁŹŒŽżÉ”Ă”œ![]() Ł»
Ł»
Łš3Ł©ÍŰŐčŃÓÉìŁș”±”ăDÔÚÖ±ÏßBCÉÏÔ˶ŻÊ±ŁŹ”±BEĄÍCEʱŁŹBE”Äł€¶ÈÊÇŚîĐĄÖ”ŁŹÓÉŁš2Ł©żÉÖȘ![]() ŁŹÔòĄśBCEÎȘ”ÈŃüÖ±œÇÈęœÇĐÎŁŹÔò
ŁŹÔòĄśBCEÎȘ”ÈŃüÖ±œÇÈęœÇĐÎŁŹÔò![]() .
.
œâŁșŁš1Ł©ÎÊÌâłőÌœŁșÈçÍŒŁŹ
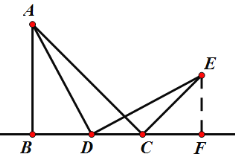
ÓÉĐęŚȘ”ÄĐÔÖÊŁŹ”ĂŁșĄÏADE=90ĄăŁŹAD=DEŁŹ
ĄàĄÏADB+ĄÏEDF=90ĄăŁŹ
ĄßĄÏABC=90ĄăŁŹ
ĄàĄÏADB+ĄÏDAB=90ĄăŁŹ
ĄàĄÏDAB=ĄÏEDFŁŹ
ĄßEFĄÍBCŁŹ
ĄàĄÏABC=ĄÏDFE=90ĄăŁŹ
ĄàĄśADBĄŐĄśDEFŁšAASŁ©Ł»
ĄàBD=EFŁŹAB=DFŁŹ
ĄàAB=DF=BCŁŹ
ĄàBD+DC=DC+CFŁŹ
ĄàBD=CF=EFŁŹ
ĄàĄśCEFÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁ»
ĄàĄÏCEF=45ĄăŁŹ
ĄàĄÏDCE=ĄÏCEF+ĄÏCFE=45Ąă+90Ąă=135ĄăŁ»
čÊŽđ°žÎȘŁșĄśADBŁŹ”ÈŃüÖ±œÇŁŹ135ĄăŁ»
Łš2Ł©ŒÌĐűÌœŸżŁșÈçÍŒŁŹčę”ăEŚśEGĄÍCDŁŹ
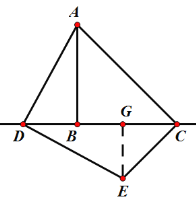
ĄßĄÏADE=ĄÏADB+ĄÏGDE=90ĄăŁŹĄÏADB+ĄÏDAB=90ĄăŁŹ
ĄàĄÏGDE=ĄÏDABŁŹ
ĄßĄÏABD=ĄÏDGE=90ĄăŁŹAD=DEŁŹ
ĄàĄśABDĄŐĄśDGEŁšAASŁ©ŁŹ
ĄàBD=GEŁŹAB=DG=BCŁŹ
ĄàBD+BG=BG+GCŁŹ
ĄàCG=BD=GEŁŹ
ĄàĄśCEGÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹ
ĄàĄÏDCE=45ĄăŁ»
Łš3Ł©ÍŰŐčŃÓÉìŁșÈçÍŒŁŹ”±”ăDÔÚÖ±ÏßBCÉÏÔ˶ŻÊ±ŁŹ”±BEĄÍCEʱŁŹBE”Äł€¶ÈÊÇŚîĐĄÖ”Ł»
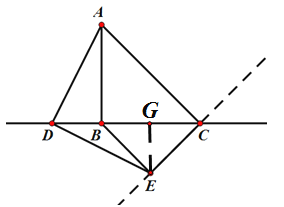
ÔòĄÏBEC=90Ąă.
ÓÉŁš2Ł©żÉÖȘŁŹĄÏDCE=45ĄăŁŹ
ĄàĄśBCEÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹ
ĄàBE=CEŁŹ
Ąß![]() ŁŹ
ŁŹ
Ąà![]() Ł»
Ł»
ĄàBE”ÄŚîĐĄÖ”ÎȘ![]() .
.