题目内容
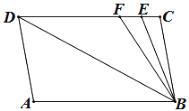
【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
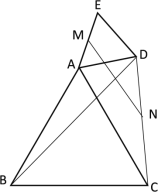
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

【答案】(1)见解析;(2)BD=DE=CE的数量关系时,△CD′E是正三角形;(3)见解析.
【解析】
(1)根据轴对称的性质得到AD=AD`,即可证明△ABD≌△ACD′
(2)由(1)可得∠BAD=∠CAD′,∠B=∠ACD′,再根据轴对称的性质得到∠EAD′+∠CAE=∠BAD+∠CAE=∠DAE=![]() ∠BAC=60°,得到△CD′E是正三角形,即可解答
∠BAC=60°,得到△CD′E是正三角形,即可解答
(3)利用勾股定理即可解答
(1)证明:∵△ADE与△AD′E是关于AE的轴对称图形,
∴AD=AD′,
在△ABD和△ACD′中,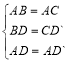 ,
,
∴△ABD≌△ACD′(SSS);
(2)解:∵△ABD≌△ACD′,
∴∠BAD=∠CAD′,∠B=∠ACD′,
∵△ADE与△AD′E是关于AE的轴对称图形,
∴∠DAE=∠EAD′,DE=ED′,
∴∠EAD′+∠CAE=∠BAD+∠CAE=∠DAE=![]() ∠BAC=60°,
∠BAC=60°,
∵△CD′E是正三角形,
∴CE=CD′=ED′,
∵BD=CD′,DE=ED′,
∴BD=DE=CE;
(3)证明:∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=∠ACD′=45°,
∴∠ECD′=90°,
∴ED′2=CD′2+EC2,
∵BD=CD′,DE=ED′,
∴DE2=BD2+EC2.

 阅读快车系列答案
阅读快车系列答案【题目】某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
某景区一周天气预报
日期 | 天气 |
7月1日 | 晴 |
7月2日 | 晴 |
7月3日 | 雨 |
7月4日 | 阴 |
7月5日 | 晴 |
7月6日 | 晴 |
7月7日 | 阴 |
(1)随机选择一天,恰好天气预报是晴;
(2)随机选择连续的两天,恰好天气预报都是晴.