题目内容
【题目】问题探究
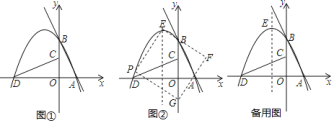
(1)如图①,在△ABC 中,∠B=30°,E 是 AB 边上的点,过点 E 作 EF⊥BC 于 F,则![]() 的值为 .
的值为 .
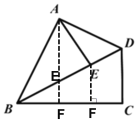
(2)如图②,在四边形 ABCD 中,AB=BC=6,∠ABC=60°,对角线 BD 平分∠ABC,点E 是对角线 BD 上一点,求 AE+ ![]() BE的最小值.
BE的最小值.
问题解决
(3)如图③,在平面直角坐标系中,直线 y -x 4 分别于 x 轴,y 轴交于点 A、B,点 P 为直线 AB 上的动点,以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C(0,-4),点 D(3,0)连接 CQ、DQ,那么DQ ![]() CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)4.
;(3)4.
【解析】
(1)利用直角三角形中,30°所对的直角边等于斜边的一半求解即可;
(2) 作EF⊥BC于F, 根据直角三角形中,30°所对的直角边等于斜边的一半,得到AE+![]() BE=AE+EF ,再根据勾股定理得到AE+
BE=AE+EF ,再根据勾股定理得到AE+![]() BE的最小值;
BE的最小值;
(3) 作PM⊥y轴于M,QN⊥y轴于N,易证△POM≌△OQN,根据当![]() 、Q、N共线时,
、Q、N共线时,![]() Q+NQ最小求解即可.
Q+NQ最小求解即可.
解;(1) ∵EF⊥BC, ∴∠BFE=90°, ∵∠B=30°, ∴![]() =
=![]() ;
;
(2)作EF⊥BC于F, ∵∠ABC=60°,对角线 BD 平分∠ABC,∴∠DBC=30°, ∴∠EF=![]() BE, ∴AE+
BE, ∴AE+![]() BE=AE+EF, ∴当点A、E、F三点在一条直线时,AE+
BE=AE+EF, ∴当点A、E、F三点在一条直线时,AE+![]() BE 最小,∵∠ABF=60°, ∴∠BAF=30°, ∵AB=6, ∴BF=
BE 最小,∵∠ABF=60°, ∴∠BAF=30°, ∵AB=6, ∴BF=![]() AB=3, ∴AF=
AB=3, ∴AF=![]() , ∴AE+
, ∴AE+![]() BE的最小值为
BE的最小值为![]() .
.
(3) ∵y=-x+4, ∴B(0,4),A(4,0),
作PM⊥y轴于M,QN⊥y轴于N, ∴∠PMO=∠QNO=90°, ∵∠POM+MPO=∠POM+∠QON=90°∴∠MPO=∠QON, ∵PO=QO, ∴△POM≌△OQN,设BM=PM=ON=t,则OM=NQ=CN=4-t, ∴无论P在任何位置△CNQ都为等腰三角形,∠NCQ=45°,则Q点永远在直线AC上,作D点关于直线AC的对称点![]() , ∵D(3,0), ∴
, ∵D(3,0), ∴![]() (4,-1),则DQ+NQ=
(4,-1),则DQ+NQ=![]() Q+NQ, ∴当
Q+NQ, ∴当![]() 、Q、N共线时,
、Q、N共线时,![]() Q+NQ最小,最小值是N
Q+NQ最小,最小值是N![]() =4.
=4.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案