题目内容
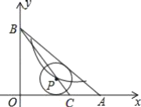
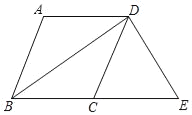
【题目】(Ⅰ)如图1,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() ,
,![]() 三点.
三点.
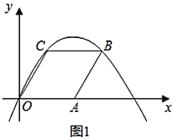
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)求抛物线的解析式.
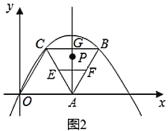
(Ⅱ)如图2,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 垂直
垂直![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
(3)当![]() 的值最小时,则点
的值最小时,则点![]() 的坐标为____________;
的坐标为____________;
(4)在(3)的条件下,连接![]() 、
、![]() 、
、![]() 得
得![]() ,问在抛物线上是否存在点
,问在抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)(1)![]() ,
, ![]() ;(Ⅰ)(2)
;(Ⅰ)(2)![]() ;(Ⅱ)(3)
;(Ⅱ)(3)![]() ;(Ⅱ)(4),存在,M点的坐标为
;(Ⅱ)(4),存在,M点的坐标为![]() 、
、![]() 、
、![]()
【解析】
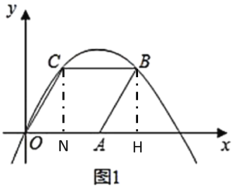
(Ⅰ)(1)过点B和点C分别是x轴的垂线于H和N,结合菱形的性质和![]() ,
,![]() ,即可求出AH,和BH及ON的长度,B点和C点坐标即可得出;
,即可求出AH,和BH及ON的长度,B点和C点坐标即可得出;
(Ⅰ)(2)把![]() ,
,![]() ,
,![]() 三点坐标代入抛物线
三点坐标代入抛物线![]() ,即可求得;
,即可求得;
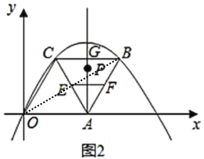
(Ⅱ)(3)由题意知AG即为抛物线的对称轴,C点的对称点为B,连接OB,(见详解图),OB与AG的交点即为P点,![]() 的最小值即为OB长度,求出OB的直线解析式,即可求出P点坐标;
的最小值即为OB长度,求出OB的直线解析式,即可求出P点坐标;
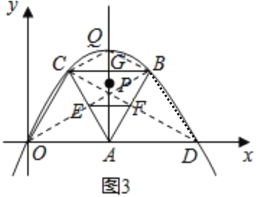
(Ⅱ)(4)由题意可知PE=PF,EF∥BC∥OD,进一步可知△PEF是底角为30°,顶角为120°的等腰三角形,设AG与抛物线交点为Q点(即为顶点),D点为O点关于对称轴的对称点,连接OB,CD,CQ,BQ,BD,再结合菱形中∠OCB=120°角,可知点O、点Q和点D即为所求M点。
(Ⅰ)(1)过点B和点C分别是x轴的垂线于H和N,
∵![]() ,
,![]() ,结合菱形的性质,
,结合菱形的性质,
∴![]() ,
,![]() ,
,
∴B点坐标为![]() ,C点坐标为
,C点坐标为![]() ,
,
故答案为:![]() ,
, ![]() ;
;
(Ⅰ)(2)将O点坐标![]() ,B点
,B点![]() ,C点坐标
,C点坐标![]() 三点坐标代入抛物线
三点坐标代入抛物线![]() ,可得:
,可得:
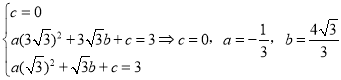
∴抛物线解析式为:![]()
(Ⅱ)(3)由题意知AG为抛物线的对称轴,C点的对称点为B,连接OB,OB与AG的交点即为P点,![]() 的最小值即为OB长度,
的最小值即为OB长度,
设OB直线为![]() ,将O点和B点坐标代入,求得:
,将O点和B点坐标代入,求得:![]() ,
,
令![]() ,y=2,
,y=2,
所以P点坐标为:![]()
(Ⅱ)(4)设AG与抛物线交点为Q点(即为顶点),D点为O点关于对称轴的对称点,连接OB,CD,CQ,BQ,BD,
∵点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点
的中点
∴可知PE=PF,EF∥BC∥OD,
∴△PEF是底角为30°,顶角为120°的等腰三角形,
在△COB与△BCD中,OC=CB=BD,∠OCB=∠CBD=120°,
∴△COB≌△BCD∽△PEF
故O点(0,0)和D点![]() 即满足M点要求;
即满足M点要求;
另在△QCB中,∠QCB=∠BOD=30°,QC=QO,
∴△QCB∽△PEF,
故Q点![]() 也满足M点要求,
也满足M点要求,
故M点的坐标为:![]() 、
、![]() 、
、![]() .
.
故答案为:(Ⅰ)(1)![]() ,
, ![]() ;(Ⅰ)(2)
;(Ⅰ)(2)![]() ;(Ⅱ)(3)
;(Ⅱ)(3)![]() ;(Ⅱ)(4),存在,M点的坐标为
;(Ⅱ)(4),存在,M点的坐标为![]() 、
、![]() 、
、![]()

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
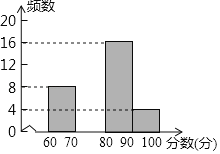
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .