题目内容
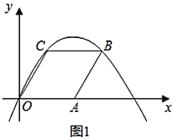
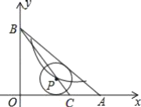
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 的圆心
的圆心![]() 在线段
在线段![]() 上,且⊙
上,且⊙![]() 与边
与边![]() ,
,![]() 都相切.若反比例函数
都相切.若反比例函数![]() (
(![]() )的图象经过圆心
)的图象经过圆心![]() ,则
,则![]() ________.
________.
【答案】![]() .
.
【解析】
设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,(见详解图)用面积法可求出⊙P的半径,然后通过等腰直角三角形的性质可求出CD,从而得到点P的坐标,即可求出k的值.
设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.
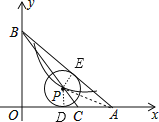
则有PD⊥OA,PE⊥AB.
设⊙P的半径为r,
∵AB=5,AC=1,
∴S△APB=![]() ABPE=
ABPE=![]() r,S△APC=
r,S△APC=![]() ACPD=
ACPD=![]() r.
r.
∵∠AOB=90°,OA=4,AB=5,
∴OB=3.
∴S△ABC=![]() ACOB=
ACOB=![]() ×1×3=
×1×3=![]() .
.
∵S△ABC=S△APB+S△APC,
∴![]() =
=![]() r+
r+![]() r.
r.
∴r=![]() .
.
∴PD=![]() .
.
又∵OB=OC=3,可知△OBC为等腰直角三角形,
∴△PDC为等腰直角三角形,
∴CD=PD=![]() .
.
∴OD=OC-CD=3-![]() =
=![]() .
.
∴点P的坐标为(![]() ,
,![]() ).
).
∵反比例函数y=![]() (k≠0)的图象经过圆心P,
(k≠0)的图象经过圆心P,
∴k=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.

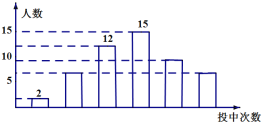
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚,对市场最为关注的产量和产量的稳定性进行了抽样调查,过程如下:
收集数据从甲、乙两个大棚中分别随机收集了相同生产周期内25株秧苗生长出的小西红柿的个数:
甲:26,32,40,51,44,74,44,63,73,74,81,54,62,41,33,54,43,34,51,63,64,73,64,54,33
乙:27,35,46,55,48,36,47,68,82,48,57,66,75,27,36,57,57,66,58,61,71,38,47,46,71
整理数据按如下分组整理样本数据:
个数(x) 株数(株) 大棚 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
甲 | 5 |
| 5 |
| 4 | 1 |
乙 | 2 | 4 |
| 6 | 5 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45≤x<65个为产量良好,65≤x<85个为产量优秀)
分析数据两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 |
| 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论
(1)补全上述表格;
(2)可以推断出 大棚的小西红柿秩苗品种更适应市场需求,理由为 (至少从两个不同的角度说明推断的合理性);
(3)估计乙大棚的300株小西红柿秧苗中产量优秀的有多少株?