题目内容
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点是
的对应点是![]() ,连接
,连接![]() ,当
,当![]() 是直角三角形时,则
是直角三角形时,则![]() 的值是________
的值是________
【答案】3或6
【解析】
分两种情况讨论:①当∠AFE=90°时,易知点F在对角线AC上,设DE=x,则AE、EF均可用x表示,在Rt△AEF中利用勾股定理构造关于x的方程即可;②当∠AEF=90°时,易知F点在BC上,且四边形EFCD是正方形,从而可得DE=CD.
解:当E点与A点重合时,∠EAF的角度最大,但∠EAF小于90°,
所以∠EAF不可能为90°,
分两种情况讨论:
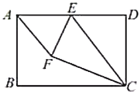
①当∠AFE=90°时,如图1所示,
根据折叠性质可知∠EFC=∠D=90°,
∴A、F、C三点共线,即F点在AC上,
∵四边形ABCD是矩形,
∴AC=![]() ,
,
∴AF=ACCF=ACCD=106=4,
设DE=x,则EF=x,AE=8x,
在Rt△AEF中,利用勾股定理可得AE2=EF2+AF2,
即(8x)2=x2+42,
解得x=3,即DE=3;
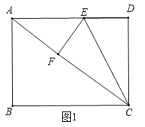
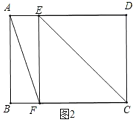
②当∠AEF=90°时,如图2所示,则∠FED=90°,
∵∠D=∠BCD=90°,DE=EF,
∴四边形EFCD是正方形,
∴DE=CD=6,
故答案为:3或6.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目