Question

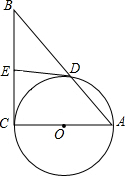如图，Rt△ABC中，∠ACB=90°，以AC为直径作⊙O，交AB于D，E为BC中点，连ED．
（1）求证：ED是⊙O的切线；
（2）若⊙O半径为3，ED=4，求AB长？

Answer 1

分析：（1）方法一：连接OD，OE，CD，利用直角三角形斜边的中线等于斜边的一半，求证∠EDC=∠ECD，再根据AC为直径作⊙O，求证∠ODC+∠EDC=∠OCD+∠ECD=90°即可．
方法二：连接OE，OD，根据E是BC的中点，∠BDC=90°，利用SSS求证△ODE≌△OCE，然后得∠ODE=∠OCE=90°即可．
（2）根据⊙O半径为3，ED=4，利用勾股定理求得OE的长，再利用三角形中位线定理即可求得AB的长．

解答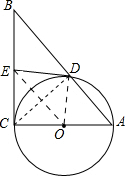：（1）证明：
方法一：连接OD，OE，CD，
∵∠ADC=90°，
∴∠CDB=90°，
∵E是BC的中点，
∴DE=CE，
∴∠EDC=∠ECD，
∵OC=OD，
∴∠ODC=∠OCD，
∴∠ODC+∠EDC=∠OCD+∠ECD=90°，
即OD⊥ED，
∴ED与⊙O相切．
方法二：连接OE，OD，
∵E是BC的中点，∠BDC=90°，
∴DE=CE，
又∵OD=OC，OE=OE，
∴△ODE≌△OCE，
∴∠ODE=∠OCE=90°，
即OD⊥ED，
∵D在⊙O上，
∴ED与⊙O相切．

（2）解：∵⊙O半径为3，即OC=3，ED=4，
∴CE=ED=4，
∴OE=

CE2+OC2

=5，
∵E为BC中点，OC=OA，
∴OE为△ACB的中位线，
∴OE=

1

2

AB，
∴AB=10．
答：AB长为10．

点评：本题主要考查了相似三角形的性质，以及切线的判定，切线的判定常用的方法是利用切线的判定定理转化为证明垂直的问题．