题目内容
问题背景:在△ABC中,AB、BC、AC三边的长分别为
、
、
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上:
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别
a、
a、
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.

| 5 |
| 10 |
| 13 |
(1)请你将△ABC的面积直接填写在横线上:
3.5
3.5
.思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别
| 5 |
| 8 |
| 17 |

分析:(1)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解;
(2)先作出以a、2a为直角边的三角形的斜边,再根据勾股定理和网格结构作出
a、
a的长度,然后顺次连接即可;再根据三角形所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
(2)先作出以a、2a为直角边的三角形的斜边,再根据勾股定理和网格结构作出
| 8 |
| 17 |
解答: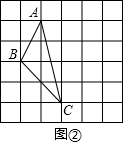 解:(1)△ABC的面积=3×3-
解:(1)△ABC的面积=3×3-
×1×2-
×1×3-
×2×3
=9-1-
-3
=9-5.5
=3.5;
故答案为:3.5;
(2)△ABC如图所示,
△ABC的面积=2a•4a-
×2a•a-
×2a•2a-
×4a•a
=8a2-a2-2a2-2a2
=3a2.
 解:(1)△ABC的面积=3×3-
解:(1)△ABC的面积=3×3-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=9-1-
| 3 |
| 2 |
=9-5.5
=3.5;
故答案为:3.5;
(2)△ABC如图所示,
△ABC的面积=2a•4a-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=8a2-a2-2a2-2a2
=3a2.
点评:本题考查了勾股定理,读懂题目信息并熟练掌握网格结构和勾股定理准确找出对应点的位置是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
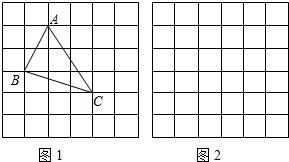
 问题背景:“在△ABC中,AB、BC、AC三边的长分别为
问题背景:“在△ABC中,AB、BC、AC三边的长分别为 问题背景:在△ABC中,AB、BC、AC三边的长分别为
问题背景:在△ABC中,AB、BC、AC三边的长分别为