题目内容

问题背景：在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
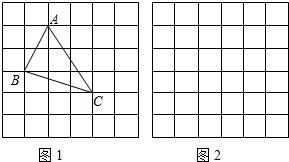，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶精英家教网点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上．
 

（2）画△DEF，DE、EF、DF三边的长分别为
2
、
8
、
10

①判断三角形的形状，说明理由．
②求这个三角形的面积．
分析：（1）利用恰好能覆盖△ABC的边长为3的小正方形的面积减去三个小直角三角形的面积即可解答；
（2）①利用勾股定理的逆定理进行解答，②利用（1）方法解答就可以解决问题．
解答：解：（1）如图，
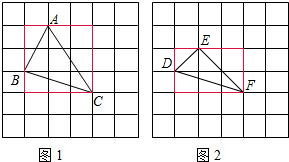
精英家教网
S△ABC=3×3-
1
2
×3×1-
1
2
×2×1-
1
2
×3×2=3.5；

（2）①△DEF为直角三角形；
因为( 
2
) 2+(
8
)2=(
10
)2，
所以△DEF为直角三角形；
②S△DEF=3×2-
1
2
×3×1-
1
2
×2×2-
1
2
×1×1=2；
答：△DEF的面积为2．
点评：此题考查勾股定理，勾股定理的逆定理以及三角形面积的计算．
练习册系列答案
相关题目
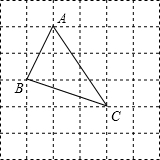问题背景：
在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积．
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上
 
；
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法．若△ABC三边的长分别为
5
a、2
2
a、
17
a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积；
探索创新：
（3）若△ABC三边的长分别为
m2+16n2
、
9m2+4n2
、2
m2+n2
（m＞0，n＞0，且m≠n），试运用构图法求出这三角形的面积．
精英家教网
问题背景：在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上：
3.5
3.5
．
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别
5
a、
8
a、
17
a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
问题背景：“在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积．”
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网络中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），
（1）如图所示．这样不需求△ABC的高，而借用网格就能计算出它的面积是
3.5
3.5
．
（2）如图我们把上述求面积的方法叫做构图法．若△DCE三边的长分别为
m2+16n2
、
9m2+4n2
、
4m2+4n2
（m＞0，n＞0，且m≠n），试运用构图法求出这三角形的面积．
问题背景：在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形BC边上的高．
杰杰同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．借用网格等知识就能计算出这个三角形BC边上的高．
（1）请在正方形网格中画出格点△ABC；
（2）求出这个三角形BC边上的高．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网