题目内容
如图所示,在△ABC中,BC=6,E,F分别是AB,AC的中点,点P在射线EF上,BP交CE于D,点Q在CE上且BQ平分∠CBP,设BP= ,PE=
,PE= .当CQ=
.当CQ= CE时,
CE时, 与
与 之间的函数关系式是 ;当CQ=
之间的函数关系式是 ;当CQ= CE(
CE( 为不小于2的常数)时,
为不小于2的常数)时, 与
与 之间的函数关系式是 .
之间的函数关系式是 . 
 ,PE=
,PE= .当CQ=
.当CQ= CE时,
CE时, 与
与 之间的函数关系式是 ;当CQ=
之间的函数关系式是 ;当CQ= CE(
CE( 为不小于2的常数)时,
为不小于2的常数)时, 与
与 之间的函数关系式是 .
之间的函数关系式是 . 
y=–x+6;y=–x+6(n–1)
试题分析:设CQ=a,DE=b,BD=c,则DP=y-c;设EQ=kCQ=ka(k>0),则DQ=ka-b,CD=(k+1)a-b.过Q点作QM⊥BC于点M,作QN⊥BP于点N,由BQ平分∠CBP,根据角平分线的性质可得QM=QN,再结合三角形的面积公式及平行线的性质即可得到结果.
如图,设CQ=a,DE=b,BD=c,则DP=y-c;
不妨设EQ=kCQ=ka(k>0),则DQ=ka-b,CD=(k+1)a-b.
过Q点作QM⊥BC于点M,作QN⊥BP于点N,
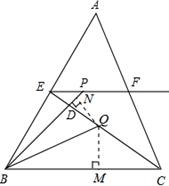
∵BQ平分∠CBP,
∴QM=QN.
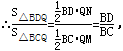
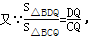
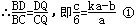
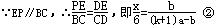
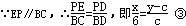
由①②③式联立解得:y="6k-x" ④
当CQ=
 CE时,k=1,
CE时,k=1,故y与x之间的函数关系式为:y=6-x
当CQ=
 CE(
CE(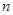 为不小于2的常数)时,k=n-1,
为不小于2的常数)时,k=n-1,由(2)中④式可知,y与x之间的函数关系式为:y=6(n-1)-x.
点评:本题采用了从一般到特殊的解题思想,简化了解答过程;同学们亦可尝试从特殊到一般的解题思路.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
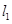 的解析式为
的解析式为 ,且
,且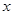 轴交于点
轴交于点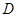 ,直线
,直线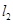 经过点
经过点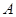 、
、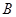 ,直线
,直线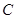 .
.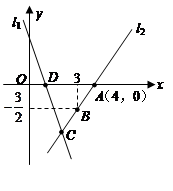
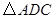 的面积;
的面积;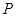 ,使得
,使得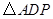 与
与 的图象向上平移,则平移后所得图象对应的函数解析式可以是 (写出一个即可).
的图象向上平移,则平移后所得图象对应的函数解析式可以是 (写出一个即可).
 千米,气温下降若干度(℃),某地空中气温
千米,气温下降若干度(℃),某地空中气温 (℃)与高度
(℃)与高度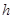 (千米)间的函数的图像如图所示那么当高度
(千米)间的函数的图像如图所示那么当高度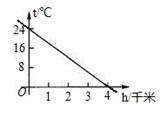
 km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程
km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程 (单位:km)与时间
(单位:km)与时间 (单位:h)之间的关系如图所示,则下列结论正确的是( )
(单位:h)之间的关系如图所示,则下列结论正确的是( )
 km/h
km/h km
km km/h
km/h h到达采访地
h到达采访地