题目内容
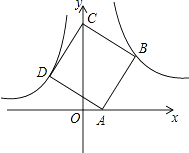
【题目】如图1,在平面直角坐标系中有一Rt△AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线l:y=﹣x2+bx+c经过A、B两点.
(1)求抛物线l的解析式及顶点G的坐标.
(2)①求证:抛物线l经过点C.
②分别连接CG,DG,求△GCD的面积.
(3)在第二象限内,抛物线上存在异于点G的一点P,使△PCD与△CDG的面积相等,请直接写出点P的坐标.
【答案】
(1)
解:∵OA=1,
∴A(1,0).
又∵tan∠BAO= ![]() =3,
=3,
∴OB=3.
∴B(0,3).
将A(1,0)、B(0,3)代入抛物线的解析式得: ![]() ,解得:b=﹣2,c=3.
,解得:b=﹣2,c=3.
∴抛物线的解析式为y=﹣x2﹣2x+3.
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的顶点G的坐标为(﹣1,4)
(2)
解:①证明:由旋转的性质可知;OC=OB=3,
∴C(﹣3,0).
当x=﹣3时,y=﹣(﹣3)2﹣2×(﹣3)+3=﹣9+6+3=0,
∴点抛物线l经过点C.
②如图1所示;过点G作GE⊥y轴.
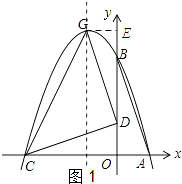
∵GE⊥y轴,G(﹣1,4),
∴GE=1,OE=4.
∴S梯形GEOC= ![]() (GE+OC)OE=
(GE+OC)OE= ![]() ×(1+3)×4=8.
×(1+3)×4=8.
∵由旋转的性质可知;OD=OA=1,
∴DE=3.
∴S△OCD= ![]() OCOD=
OCOD= ![]() ×3×1=
×3×1= ![]() ,S△GED=
,S△GED= ![]() EGED=
EGED= ![]() ×1×3=
×1×3= ![]() .
.
∴S△CDG=S梯形GEOC﹣S△OCD﹣S△GED=8﹣ ![]() ﹣
﹣ ![]() =5
=5
(3)
解:如图2所示:过点G作PG∥CD,交抛物线与点P.

∵PG∥CD,
∴△PCD的面积=△GCD的面积.
∵OD=OA=1,
∴D(0,1).
设直线CD的解析式为y=kx+b.
∵将点C(﹣3,0)、D(0,1)代入得: ![]() ,解得:k=
,解得:k= ![]() ,b=1,
,b=1,
∴直线CD的解析式为y= ![]() +1.
+1.
∵PG∥CD,
∴直线PG的一次项系数为 ![]() .
.
设PG的解析式为y= ![]() x+b1.
x+b1.
∵将点G的坐标代入得: ![]() +b1=4,解得:b1=
+b1=4,解得:b1= ![]() ,
,
∴直线PG的解析式为y= ![]() +
+ ![]() .
.
∵将y= ![]() +
+ ![]() 与y=﹣x2﹣2x+3联立.解得:
与y=﹣x2﹣2x+3联立.解得: 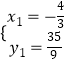 ,
, ![]() ,
,
∴P(﹣ ![]() ,
, ![]() )
)
【解析】(1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式,可求得b、c的值,从而可得到抛物线的解析式,最后依据配方法可求得点G的坐标(2)由旋转的性质可求得点D和点C的坐标,将点C的横坐标代入抛物线的解析式求得y=0,从而可证明点抛物线l经过点C;如图1所示;过点G作GE⊥y轴,分别求得梯形GEOC、△OCD、△GED的面积,最后依据S△CDG=S梯形GEOC﹣S△OCD﹣S△GED求解即可;(3)如图2所示:过点G作PG∥CD,交抛物线与点P.先求得直线CD的解析式,然后可得到直线PG的一次项系数,然后由点G的坐标可求得PG的解析式,最后将直线PG的解析式与抛物线的解析式联立,最后解得点P的坐标即可.

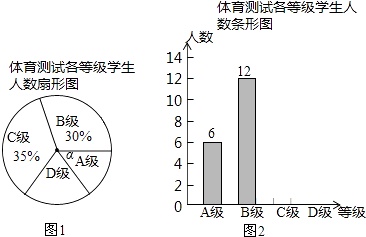
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5. 月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?