Question

【题目】如图1，在ABCD中，对角线AC与BD相交于点O，经过点O的直线与边AB相交于点E，与边CD相交于点F．
（1）求证：OE=OF；
（2）如图2，连接DE，BF，当DE⊥AB时，在不添加其他辅助线的情况下，直接写出腰长等于 BD的所有的等腰三角形．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴OA=OC，AB∥CD，OB=OD，

∴∠OAE=∠OCF，

在△OAE和△OCF中， ，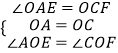

∴△AOE≌△COF（ASA），

∴OE=OF

（2）解：∵OE=OF，OB=OD，

∴四边形DEBF是平行四边形，

∵DE⊥AB，

∴∠DEB=90°，

∴四边形DEBF是矩形，

∴BD=EF，

∴OD=OB=OE=OF= BD，

∴腰长等于 BD的所有的等腰三角形为△DOF，△FOB，△EOB，△DOE

【解析】（1）由四边形ABCD是平行四边形，可得OA=OC，AB∥CD，则可证得△AOE≌△COF（ASA），继而证得OE=OF；（2）证明四边形DEBF是矩形，由矩形的性质和等腰三角形的性质即可得出结论．
【考点精析】本题主要考查了等腰三角形的性质和平行四边形的性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．