题目内容
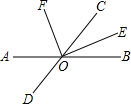如图，直线AB，CD相交于点O，OE是∠COB的平分线，FO⊥OE，已知∠AOD=70°．（1）求∠BOE的度数；
（2）OF平分∠AOC吗？为什么？
分析：由已知条件和观察图形可知∠BOC与∠AOD是对顶角，∠FOC与∠COE互余，OE是∠COB的平分线，利用这些关系可解此题．
解答：解：（1）根据对顶角相等得，∠BOC=∠AOD=70°，
∵OE是∠COB的平分线，
∴∠BOE=
∠BOC=35°．
（2）∵∠AOD=70°，∴∠AOC=110°，
而∠FOC=90°-∠COE=90°-35°=55°，所以OF平分∠AOC．
∵OE是∠COB的平分线，
∴∠BOE=
| 1 |
| 2 |
（2）∵∠AOD=70°，∴∠AOC=110°，
而∠FOC=90°-∠COE=90°-35°=55°，所以OF平分∠AOC．
点评：本题利用垂直的定义，对顶角和邻补角的性质计算，要注意领会由垂直得直角这一要点．
练习册系列答案
相关题目
21、如图，直线AB、CD、EF都经过点O，且AB⊥CD，∠COE=35°，求∠DOF、∠BOF的度数．
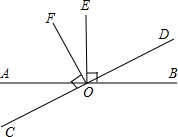如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD．
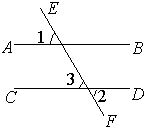25、完成推理填空：如图：直线AB、CD被EF所截，若已知AB∥CD，
如图，直线AB、CD、EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=24°，∠COG的度数=
如图，直线AB，CD相交于O点，EO⊥CD，垂足为O点，若∠BOE=50°，求∠AOD的度数．