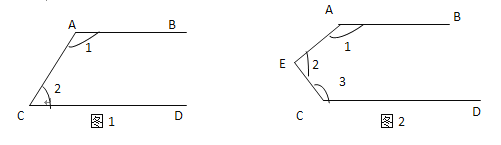��Ŀ����
����Ŀ����ͼ(1)��AB��CD�������BPD���B.��D�Ĺ�ϵ��˵�����ɣ�(��ʾ�������ε��ڽǺ͵���180��)
����ջ���д����
�⣺�����BPD+��B+��D=360��
���ɣ�����P��EF��AB��
���B+��BPE=180��______
��AB��CD��EF��AB��
��______��_____��(�������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ��)
���EPD+______=180��
���B+��BPE+��EPD+��D=360��
���B+��BPD+��D=360��
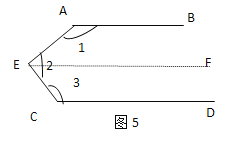
����������Ľ��ⷽ�����۲�ͼ(2)����֪AB��CD������ͼ�еġ�BPD���B.��D�Ĺ�ϵ����˵�����ɣ�
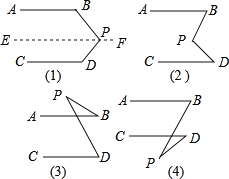
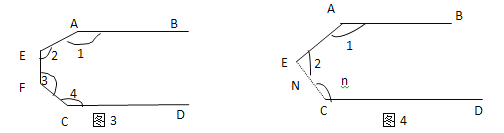
�۹۲�ͼ(3)��(4)����֪AB��CD��ֱ��д��ͼ�еġ�BPD���B.��D�Ĺ�ϵ����˵�����ɣ�
���𰸡���
��ֱ��ƽ�У�ͬ���ڽǻ�����CD��EF����CDP�ڲ����BPD����B����D�����ɼ������ۣ�3����BPD����B����D����4����BPD����B��D.
��������
�ٹ���P��EF��AB��������ֱ��ƽ�У�ͬ���ڽǻ�����֤�����ۣ�
����ٵķ������ƣ�����P��EP��AB��������ֱ��ƽ�У��ڴ�����ȣ�֤�����ۣ�
�۸���ƽ���ߵ����ʼ���������Ƕ���������⣮
�ٲ����BPD����B����D��360��
���ɣ�����P��EF��AB��
���B����BPE��180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
��AB��CD��EF��AB��
��CD��EF�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У�
���EPD����CDP��180��
���B����BPE����EPD����D��360��
���B����BPD����D��360��
�����ֱ��ƽ�У�ͬ���ڽǻ�����CD��EF����CDP
�ڲ����BPD����B����D
���ɣ�����P��EP��AB��
���B����BPE����ֱ��ƽ�У�ͬλ����ȣ�
��AB��CD��EF��AB��
��CD��EF�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У�
���EPD����D
���BPD����B����D

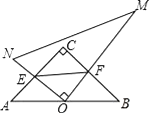
����ͼ��3����PD��AB����O�㣬
��AB��CD�����D=��AOP��
�ߡ�AOP=��BPD����B��
���BPD����B����D��
����BPD����B����D�Ĺ�ϵΪ��BPD����B����D��
��ͼ��4����PB��CD����O�㣬
��AB��CD�����B=��COP��
�ߡ�COP=��BPD����D��
���BPD����D����B��
����BPD����B����D�Ĺ�ϵΪ��BPD����B��D.