题目内容
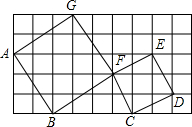
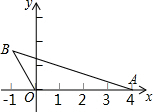
如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标______.
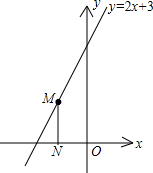

当M运动到(-1,1)时,ON=1,MN=1,
∵MN⊥x轴,所以由ON=MN可知,(0,0)就是符合条件的一个P点;
又当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有-x=-(2x+3),
解得x=-3,所以点P坐标为(0,-3).
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有-x=-
(2x+3),
化简得-2x=-2x-3,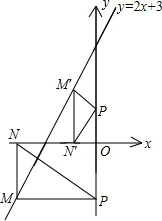
这方程无解,所以这时不存在符合条件的P点;
又当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而OP=
M′N′,
∴有-x=
(2x+3),
解得x=-
,这时点P的坐标为(0,
).
因此,其他符合条件的点P坐标是(0,0),(0,
),(0,-3),(0,1).
故本题答案为:(0,0),(0,
),(0,-3).
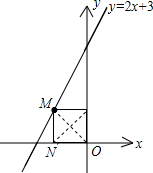
∵MN⊥x轴,所以由ON=MN可知,(0,0)就是符合条件的一个P点;
又当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有-x=-(2x+3),
解得x=-3,所以点P坐标为(0,-3).
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有-x=-
| 1 |
| 2 |
化简得-2x=-2x-3,

这方程无解,所以这时不存在符合条件的P点;
又当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而OP=
| 1 |
| 2 |
∴有-x=
| 1 |
| 2 |
解得x=-
| 3 |
| 4 |
| 3 |
| 4 |
因此,其他符合条件的点P坐标是(0,0),(0,
| 3 |
| 4 |
故本题答案为:(0,0),(0,
| 3 |
| 4 |


练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目