题目内容
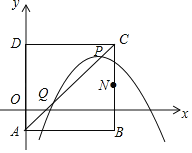
【题目】如图,已知:二次函数y=x2+bx的图象交x轴正半轴于点A,顶点为P,一次函数y=![]() x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为
x﹣3的图象交x轴于点B,交y轴于点C,∠OCA的正切值为![]() .
.
(1)求二次函数的解析式与顶点P坐标;
(2)将二次函数图象向下平移m个单位,设平移后抛物线顶点为P′,若S△ABP=S△BCP,求m的值.

【答案】(1)解析式为y=x2﹣2x,顶点P的坐标为(1,﹣1);(2)m=![]() 或m=
或m=![]() .
.
【解析】
(1)先由直线解析式求出点B,C坐标,利用∠OCA正切值求得点A坐标,再利用待定系数法求解可得;
(2)由平移知点P`坐标为(1,-1-m),设抛物线对称轴与x轴交于点H,与BC交于点M
知M(1,- ![]() ),先得出S△ABP′=
),先得出S△ABP′=![]() ABP′H=
ABP′H=![]() ×4(m+1)=2(m+1),S△BCP′=S△P′MC+S△P′MB=
×4(m+1)=2(m+1),S△BCP′=S△P′MC+S△P′MB=![]() P′MOB=3|
P′MOB=3|![]() ﹣m|,根据S△ABP=S△BCP列出方程求解可得
﹣m|,根据S△ABP=S△BCP列出方程求解可得
解:(1)∵y=![]() x﹣3,
x﹣3,
∴x=0时,y=﹣3,
当y=0时,![]() x﹣3=0,解得x=6,
x﹣3=0,解得x=6,
∴点B(6,0),C(0,﹣3),
∵tan∠OCA=![]() ,
,
∴OA=2,即A(2,0),
将A(2,0)代入y=x2+bx,得4+2b=0,
解得b=﹣2,
∴y=x2﹣2x=(x﹣1)2﹣1,
则抛物线解析式为y=x2﹣2x,顶点P的坐标为(1,﹣1);
(2)如图,
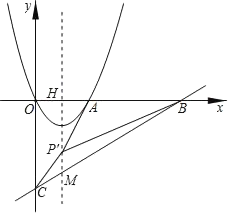
由平移知点P′坐标为(1,﹣1﹣m),
设抛物线对称轴与x轴交于点H,与BC交于点M,则M(1,﹣![]() ),
),
S△ABP′=![]() ABP′H=
ABP′H=![]() ×4(m+1)=2(m+1),
×4(m+1)=2(m+1),
S△BCP′=S△P′MC+S△P′MB=![]() P′MOB=
P′MOB=![]() |﹣1﹣m+
|﹣1﹣m+![]() |×6=3|
|×6=3|![]() ﹣m|,
﹣m|,
∴2(m+1)=3|![]() ﹣m|,
﹣m|,
解得m=![]() 或m=
或m=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目