题目内容
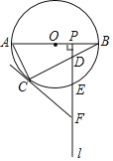
【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为16米,拱高(CD)为4米,求:
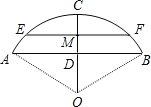
(1)桥拱半径.
(2)若大雨过后,桥下河面宽度(EF)为12米,求水面涨高了多少?
【答案】(1)10m;(2)2m.
【解析】
(1)由垂径定理可求得AD的长度,OD=OC-CD,AO=CO,在Rt△ADO中,利用勾股定理求得桥拱半径AO;(2)求水面涨高了多少实际是求DM的长度,建立直角三角形,连接EO,EF=12,由垂径定理求得EM长,利用勾股定理把MO求出来,因为CO,CD已知,所以OD可求,OM-OD即为所求DM长.
(1)∵拱桥的跨度AB=16m,∴AD=8m,
因为拱高CD=4m,利用勾股定理可得:AO2-(OC-CD)2=82,
解得OA=10(m).
所以桥拱半径为10m;
(2)设河水上涨到EF位置(如图所示),
这时EF=12m,EF∥AB,有OC⊥EF(垂足为M),
∴EM=![]() EF=6m,
EF=6m,
连接OE,则有OE=10m,
OM2=OE2-EM2=102-62=64,
所以OM=8(m)OD=OC-CD=10-4=6(m),OM-OD=8-6=2(m).
即水面涨高了2m.

练习册系列答案
相关题目