Question

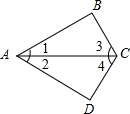
如图，在△ABC中，AB=AC，AC的中垂线交CB于D，E为AC上一点，将△CDE沿DE翻折后点C恰好与AB上一点F重合，且∠AFE=20°，则∠B的度数为（　　）

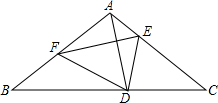
A．20°

B．30°

C．35°

D．40°

Answer 1

∵在△ABC中，AB=AC，
∴∠B=∠C．
又∵AC的中垂线交CB于D，
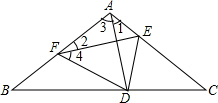
∴AD=CD，∠1=∠C．
∵根据折叠的性质知，FD=CD，∠4=∠C，
∴FD=AD，∠B=∠C=∠1=∠4，
∴∠3=∠2+∠4=∠2+∠B．
∴在△ABC中，∠1+∠3+∠B+∠C=∠B+∠2+∠B+∠B+∠B=180°，即4∠B+∠2=180°．
∵∠AFE=20°，即∠2=20°，
∴∠B=

180°-20°

4

=40°．
故选D．