题目内容
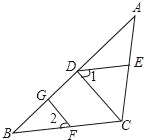
【题目】如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cos A的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】先根据等腰三角形的性质与判定以及三角形内角和定理得出∠EBC=36°,∠BEC=72°,AE=BE=BC.再证明△BCE∽△ABC,根据相似三角形的性质列出比例式![]() ,求出AE,然后在△ADE中利用余弦函数定义求出cosA的值.
,求出AE,然后在△ADE中利用余弦函数定义求出cosA的值.
∵△ABC中,AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,∠A=36°,
∵D是AB中点,DE⊥AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC-∠ABE=36°,
∠BEC=180°-∠EBC-∠C=72°,
∴∠BEC=∠C=72°,
∴BE=BC,
∴AE=BE=BC.
设AE=x,则BE=BC=x,EC=4-x.
在△BCE与△ABC中,![]()
∴△BCE∽△ABC,
∴![]() ,即
,即![]()
解得x=-2±2![]() (负值舍去),
(负值舍去),
∴AE=-2+2![]()
在△ADE中,∵∠ADE=90°,
∴cosA=![]()
故选:C

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.