题目内容
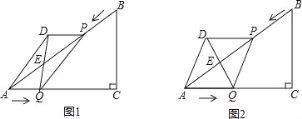
【题目】如图1,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)用含有t的代数式表示AE= .
(2)当t为何值时,平行四边形AQPD为矩形.
(3)如图2,当t为何值时,平行四边形AQPD为菱形.
【答案】
(1)AE=![]() AP=5﹣t;
AP=5﹣t;
(2)当t=![]() 时,AQPD是矩形;
时,AQPD是矩形;
(3)当t=![]() 时,□AQPD是菱形.
时,□AQPD是菱形.
【解析】
试题分析:(1)首先利用勾股定理求得AB=10,然后表示出AP,利用平行四边形对角线互相平分表示出线段AE即可;
(2)利用矩形的性质得到△APQ∽△ABC,利用相似三角形对应边的比相等列出比例式即可求得t值;
(3)利用菱形的性质得到.
试题解析:(1)∵Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.∴由勾股定理得:AB=10cm,
∵点P由B出发沿BA方向向点A匀速运动,速度均为2cm/s,∴BP=2tcm,
∴AP=AB﹣BP=10﹣2t,∵四边形AQPD为平行四边形,∴AE=![]() AP=5﹣t;
AP=5﹣t;
(2)当AQPD是矩形时,PQ⊥AC,∴PQ∥BC,∴△APQ∽△ABC,∴![]() ,即
,即![]() ,解之 t=
,解之 t=![]() .∴当t=
.∴当t=![]() 时,AQPD是矩形;
时,AQPD是矩形;
(3)当AQPD是菱形时,DQ⊥AP,则 COS∠BAC=![]() =
=![]() ,即
,即![]() ,解之 t=
,解之 t=![]()
∴当t=![]() 时,□AQPD是菱形.
时,□AQPD是菱形.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目