题目内容
如图，AD是△ABC的角平分线，过点D作DE∥AB，DF∥AC，分别交AC、AB于点E和F．
1.在图中画出线段DE和DF；
2.连接EF，则线段AD和EF互相垂直平分，这是为什么？
【答案】
1.见解析
2.见解析
【解析】(1)根据题意作图
(2)通过已知证得平行四边形AEDF是菱形，即可得出结论
解(1)如图所示；
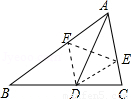
(2)∵DE∥AB，DF∥AC，
∴四边形AEDF是平行四边形，
∵AD是△ABC的角平分线，
∴∠FAD＝∠EAD，
∵AB∥DE，
∴∠FAD＝∠EDA，
∴∠EAD＝∠EDA，
∴EA＝ED，
∴平行四边形AEDF是菱形，
∴AD与EF互相垂直平分．
练习册系列答案
名校课堂系列答案
相关题目
如图，AD是△ABC是角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G，则AD与EF的位置关系是
16、已知：如图，AD是△ABC的角平分线，且 AB：AC=3：2，则△ABD与△ACD的面积之比为
如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm．
如图，AD是△ABC的中线，CE是△ACD的中线，DF是△CDE的中线，如果△DEF的面积是2，那么△ABC的面积为（ ）