题目内容
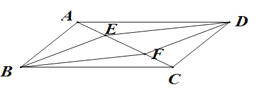
【题目】如图，在
中，
，
，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，求
、
和
的度数．
【答案】120°
【解析】
试题在△ABC中，∠ABC=66°，∠ACB=54°，根据三角形的内角和定理可得∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°．又因BE是AC边上的高，所以∠AEB=90°，即可得∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°．同理即可得∠ACF=30°，利用三角形外角的性质可得∠BHC=∠BEC+∠ACF=90°+30°=120°．
试题解析：解：∵∠ABC=66°，∠ACB=54°，
∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°．
又∵BE是AC边上的高，所以∠AEB=90°，
∴∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°．
同理，∠ACF=30°，
∴∠BHC=∠BEC+∠ACF=90°+30°=120°．
练习册系列答案
阅读快车系列答案
相关题目
