题目内容
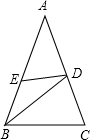 如图,AB﹦AC,BD﹦BC,AD﹦DE﹦BE,则∠A﹦
如图,AB﹦AC,BD﹦BC,AD﹦DE﹦BE,则∠A﹦分析:根据三角形的内角和定理、等腰三角形的性质,设未知数求解.
解答: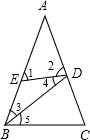 解:如图:在△ABC与△BCD中,AB﹦AC,BD﹦BC
解:如图:在△ABC与△BCD中,AB﹦AC,BD﹦BC
∴
=
,∠ABC=∠C=∠BDC
∴△ABC∽△BCD,∠A=∠5----(1)
设∠C=x,在△ABC中∠A+∠ABC+∠C=180°,即
∠A+2x=180°----(2)
在△EBD中,∠3=∠ABC-∠5=x-∠5
∵DE﹦BE
∴∠3=∠4=x-∠5
∵AD﹦DE
∴∠1=∠A
∠2=180°-∠1-∠A=180°-2∠A
∵∠BED是△AED的外角
∴∠BED=∠A+∠2=180°-∠A
在△BDE中
∠3+∠4+∠BED=180°
即2(x-∠5)+180°-∠A=180°---(3)
由(1)(2)(3)解得∠A=45°.
 解:如图:在△ABC与△BCD中,AB﹦AC,BD﹦BC
解:如图:在△ABC与△BCD中,AB﹦AC,BD﹦BC∴
| AB |
| BD |
| AC |
| BC |
∴△ABC∽△BCD,∠A=∠5----(1)
设∠C=x,在△ABC中∠A+∠ABC+∠C=180°,即
∠A+2x=180°----(2)
在△EBD中,∠3=∠ABC-∠5=x-∠5
∵DE﹦BE
∴∠3=∠4=x-∠5
∵AD﹦DE
∴∠1=∠A
∠2=180°-∠1-∠A=180°-2∠A
∵∠BED是△AED的外角
∴∠BED=∠A+∠2=180°-∠A
在△BDE中
∠3+∠4+∠BED=180°
即2(x-∠5)+180°-∠A=180°---(3)
由(1)(2)(3)解得∠A=45°.
点评:本题考查了三角形内角和定理及内角与外角的关系.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 24、如图,AB=AC=AD.
24、如图,AB=AC=AD. (2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.
(2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.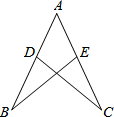 (2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是
(2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是 如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.
如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数. 如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求:
如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求: