��Ŀ����
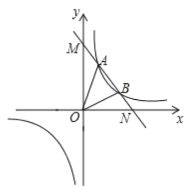
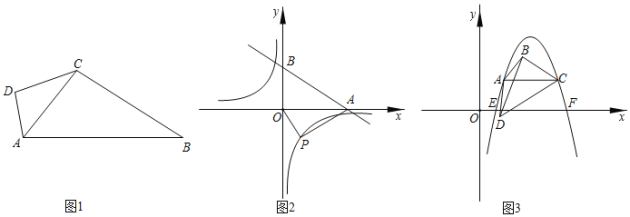
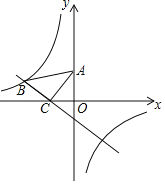
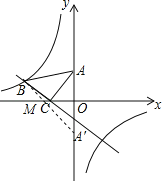
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ���C����Ϊ����1��0������A����Ϊ��0��2����һ�κ���y��kx+b��ͼ����B��C������������y��![]() ��ͼ����B��
��ͼ����B��
��1����һ�κ����ͷ����������Ĺ�ϵʽ��
��2��ֱ��д����x��0ʱ��kx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��
��3����x������һ��M��ʹ��AM+BM��ֵ��С��ֱ��д����M�������AM+BM����Сֵ��
���𰸡���1��y����![]() x��
x��![]() ��y����
��y����![]() ����2����3��x��0����3����M������Ϊ����2��0����AM+BM����СֵΪ3
����2����3��x��0����3����M������Ϊ����2��0����AM+BM����СֵΪ3![]() ��
��
��������
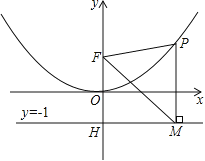
��1������B��BF��x���ڵ�F������AOC�ա�CFB��õ�B�����꣬���ô���ϵ���������һ�κ����ͷ����������Ĺ�ϵʽ��
��2����x��0ʱ�����һ�κ���ֵy��kx+bС�ڷ���������y��![]() ��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��3��������ԳƵ����ʣ��ҵ���A����x�ĶԳƵ�A��������BA������BA����x��Ľ��㼴Ϊ��M��λ�ã����ֱ��BA���Ľ���ʽ���ɵó���M�����꣬����B��A������������AM+BM����Сֵ��
�⣺��1������B��BF��x���ڵ�F��
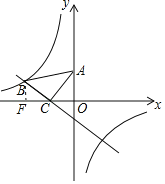
�ߵ�C����Ϊ(��1,0)����A����Ϊ��0,2����
��OA��2��OC��1��
�ߡ�BCA��90����
���BCF+��ACO��90����
�֡ߡ�CAO+��ACO��90����
���BCF����CAO��
����AOC����CFB��
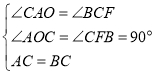
���AOC�ա�CFB��AAS����
��FC��OA��2��BF��OC��1��
���B����������3��1����
����B��������뷴������������ʽ�ɵã� ![]() ��
��
��ã�k����3��
�ʿɵ÷�������������ʽΪy����![]() ��
��
����B��C���������һ�κ�������ʽ�ɵã�![]() ��
��
��ã�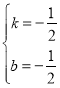 ��
��
�ʿɵ�һ�κ�������ʽΪ![]() ��
��
��2����ϵ�B�����꼰ͼ�ɵõ�x��0ʱ��![]() ��0�Ľ⼯Ϊ����3��x��0��
��0�Ľ⼯Ϊ����3��x��0��
��3������A����x��ĶԳƵ�A�������� B A����x�� �Ľ��㼴Ϊ��M��
��A��0��2��������A����x��ĶԳƵ�A����
��A����0����2����
��ֱ��BA���Ľ���ʽΪy��ax+b������A������B���������ɵã�![]()
��ã�![]() ��
��
��ֱ��BA���Ľ���ʽΪy����x��2��
��y��0���ɵé�x��2��0��
��ã�x����2��
�ʵ�M ������Ϊ����2��0����
AM+BM��BM+MA����BA����![]() ��
��
���Ͽɵã���M������Ϊ����2��0����AM+BM����СֵΪ![]() ��
��