题目内容
【题目】观察图,解答下列问题.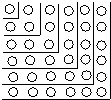
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?
(2)某一层上有65个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22 ,
由此得,1+3=22 .
同样,
由前三层的圆圈个数和得:1+3+5=32 .
由前四层的圆圈个数和得:1+3+5+7=42 .
由前五层的圆圈个数和得:1+3+5+7+9=52 .
…
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1+3+5+…+99的和;
(5)计算:101+103+105+…+199的和.
【答案】
(1)解:第八层有15个小圆圈,第n层有(2n﹣1)个小圆圈
(2)解:令2n﹣1=65,
得,n=33.
所以,这是第33层
(3)解:1+3+5+…+(2n﹣1)=n2
(4)解:1+3+5+…+99=502=2500
(5)解:101+103+105+…+199=(1+3+5+…+199)﹣(1+3+5+…+99)
=1002﹣502
=7500
【解析】(1)根据题意可知每一层圆圈个数是连续奇数,则第n层为2n+1;(2)由(1)和已知条件某一层上有65个圆圈可列方程求解;(3)根据已知条件可得1+3+5+…+(2n﹣1)=n2;(4)由(3)可得1+3+5+…+99=502;(5)将101+103+105+…+199转化成(1+3+5+…+199)﹣(1+3+5+…+99)求解即可。

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目