题目内容
【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.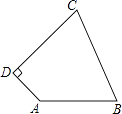
【答案】解:连接AC,过点C作CE⊥AB于点E. 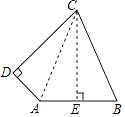
∵AD⊥CD,
∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,
AC= ![]() =
= ![]() =13.
=13.
∵BC=13,
∴AC=BC.
∵CE⊥AB,AB=10,
∴AE=BE= ![]() AB=
AB= ![]() ×10=5.
×10=5.
在Rt△CAE中,
CE= ![]() =
= ![]() =12.
=12.
∴S四边形ABCD=S△DAC+S△ABC= ![]() ×5×12+
×5×12+ ![]() ×10×12=30+60=90.
×10×12=30+60=90.
【解析】抓住题中关键的已知条件,AD⊥CD及CD=12,AD=5,因此连接AC,利用勾股定理求出AC的长,即可得出AC=BC,可知△CAB是等腰三角形,由此添加辅助线过点C作CE⊥AB于点E,利用勾股定理求出△CAB的高CE,要求四边形ABCD的面积,就转化为求△CAB和△ACD的面积,即可求解。
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对等腰三角形的判定的理解,了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.

 名校课堂系列答案
名校课堂系列答案【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
= ![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2 ![]() ,则⊙O的半径为( )
,则⊙O的半径为( ) 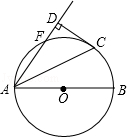
A.2 ![]()
B.4 ![]()
C.2
D.4
【题目】列方程解应用题
(1)一个学生有中国邮票和外国邮票共25张,中国邮票的张数比外国邮票的张数的2倍少2张,这个学生有中国邮票和外国邮票各多少张?
(2)甲乙二人相距18千米,二人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可以追上乙。求二人的平均速度各是多少?
(3)国家为九年义务教育期间的学生实行“两免一补”政策,下表是某地区某中学国家免费提供教科书补助的部分情况。
| 七 | 八 | 九 | 合计 |
每人免费补助金额(元) | 110 | 90 | 50 | —— |
人数(人) | 80 | 300 | ||
免费补助金额(元) | 4000 | 26200 |
请问该校七、八年级各有学生多少人?