Question

【题目】有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有2个完全相同的小球，分别标有数字﹣1，﹣2．现从甲袋中随机抽取一个小球，将标有的数字记录为x，再从乙袋中随机抽取一个小球，将标有的数字记录为y，确定点M的坐标为（x，y）．

（1）用树状图或列表法列举点M所有可能的坐标；

（2）求点M（x，y）在二次函数y=x2﹣2x﹣2的图象上的概率．

Answer 1

【答案】（1）见解析；（0，﹣1），（0，﹣2），（1，﹣1），（1，﹣2），（2，﹣1），（2，﹣2）；（2）．

【解析】

试题分析：（1）画树状图可展示所有6种等可能的结果数；

（2）根据二次函数图象上点的坐标特征可判断M（x，y）在二次函数y=x2﹣2x﹣2的图象上的结果数，然后根据概率公式求解．

解：（1）画树状图为：

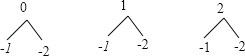
共有6种等可能的结果数，它们为（0，﹣1），（0，﹣2），（1，﹣1），（1，﹣2），（2，﹣1），（2，﹣2）；

（2）点M（x，y）在二次函数y=x2﹣2x﹣2的图象上的结果数为2，

所以点M（x，y）在二次函数y=x2﹣2x﹣2的图象上的概率==．