题目内容
如图,已知△ABC中,AB=BC=1,ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时钟方向旋转.
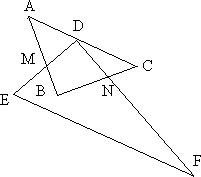
(1)在图1中,DE交AB于点M,DF交BC于点N.
①证明:DM=DN
②在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的;若不发生变化,求出其面积.
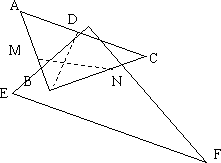
(2)在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的周长是否发生变化?若发生变化,求出最大值或最小值是多少?若不发生变化,求出其周长.
答案:
解析:
解析:
|
(1)①证明:连结DB.在Rt△ABC中,AB=BC,AD=CD.
∴DB=DC=AD,∠BDC=90°. ∴∠A=∠DBN=45°. ∵∠ADM+∠MDB=∠BDN+∠MDB=90°, ∴∠ADM=∠BDN. ∴△ADM≌△BDN. ∴DM=DN(方法不唯一) ②四边形DMBN的面积不发生变化. 由①,知△BMD≌△CND.∴S△BMD=S△CND ∴S四边形DMBN=S△DBN+S△DMB=S△DBN+S△DNC=S△DBC= (2)四边形DMBN的周长发生变化. 由①的三角形全等的证明,可知AM=BN,BM=CN.故可设BM=x,BN=1-x,由勾股定理得 四边形DMBN的周长为BM+BN+DM+DN=x+(1-x)+ ∵0<x<1,∴当 |

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.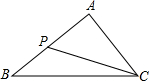 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )