Question

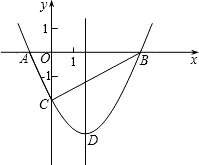如图，抛物线y=

1

2

x²+bx-2与x轴交于A、B两点，与y轴交于C点，且A（-1，0）．
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M（m，0）是x轴上的一个动点，当MC+MD的值最小时，求m的值．
[注：抛物线y=ax²+bx+c的顶点坐标为（-

b

2a

，

4ac-b2

4a

）．]．

Answer 1

分析：（1）因为点A在抛物线上，所以将点A代入函数解析式即可求得；
（2）由函数解析式可以求得其与x轴、y轴的交点坐标，即可求得AB、BC、AC的长，由勾股定理的逆定理可得三角形的形状；
（3）首先可求得二次函数的顶点坐标，再求得C关于x轴的对称点C′，求得直线C′D的解析式，与x轴的交点的横坐标即是m的值．

解答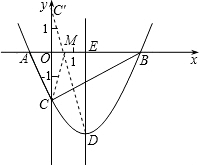：解：（1）∵点A（-1，0）在抛物线y=

1

2

x²+bx-2上，
∴

1

2

×（-1）²+b×（-1）-2=0，b=-

3

2

∴抛物线的解析式为y=

1

2

x²-

3

2

x-2
y=

1

2

x²-

3

2

x-2=

1

2

（x²-3x-4）=

1

2

（x-

3

2

）²-

25

8

，
∴顶点D的坐标为（

3

2

，-

25

8

）．（4分）

（2）当x=0时y=-2，
∴C（0，-2），OC=2．
当y=0时，

1

2

x²-

3

2

x-2=0，
∴x₁=-1，x₂=4，
∴B（4，0）．（6分）
∴OA=1，OB=4，AB=5．
∵AB²=25，AC²=OA²+OC²=5，BC²=OC²+OB²=20，
∴AC²+BC²=AB²．
∴△ABC是直角三角形．  （8分）

（3）作出点C关于x轴的对称点C′，则C′（0，2），OC′=2
连接C′D交x轴于点M，
根据轴对称性及两点之间线段最短可知，MC+MD的值最小．  （9分）
解法一：设抛物线的对称轴交x轴于点E．
∵ED∥y轴，
∴∠OC′M=∠EDM，∠C′OM=∠DEM
∴△C′OM∽△DEM．
∴

OM

EM

=

OC′

ED

∴

m

3 2 -m

=

2

25 8

，
∴m=

24

41

12分
解法二：设直线C′D的解析式为y=kx+n，
则

n=2 3 2 k+n=- 25 8

，
解得n=2，k=-

41

12

．
∴y=-

41

12

x+2．
∴当y=0时，-

41

12

x+2=0，x=

24

41

．
∴m=

24

41

．  （12分）

点评：此题考查了待定系数法求解析式，考查了二次函数与一次函数的综合应用，解题时要注意数形结合思想的应用．