题目内容
【题目】阅读材料:在数轴上表示两个数![]() 的点之间的距离可以表示为
的点之间的距离可以表示为![]() ,比如表示3的点与-2的点之间的距离表示为
,比如表示3的点与-2的点之间的距离表示为![]() ;
;![]() 可以表示数
可以表示数![]() 的点与表示数1的点之间的距离与表示数
的点与表示数1的点之间的距离与表示数![]() 的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
![]()
(1)解方程![]()
(2)![]() 的最小值是 .
的最小值是 .
(3)![]() 的最小值是 此时
的最小值是 此时![]() 的值为 .
的值为 .
拓展推广:如图所示:当表示数![]() 的点在点
的点在点![]() 和点
和点![]() 之间(包含点
之间(包含点![]() 和点
和点![]() )时,表示数
)时,表示数![]() 的点与点
的点与点![]() 的距离与表示数
的距离与表示数![]() 的点和点
的点和点![]() 的距离之和最小,且最小值为3,即
的距离之和最小,且最小值为3,即![]() 的最小值是3,且此时
的最小值是3,且此时![]() 的取值范围为
的取值范围为
(4)已知数![]() 满足
满足![]() 则
则![]()
(5)当![]() 的最小值是4.5时,求出
的最小值是4.5时,求出![]() 的值及对应
的值及对应![]() 的值或取值范围.
的值或取值范围.
【答案】(1)x=-1或x=-3(2)8;(3)5; 0;拓展推广: -2≤x≤1;(4)-9;8;(5)a=3.5,x=0或a=-4.5, x=-1.
【解析】
(1)根据题意及绝对值的含义即可求解;
(2)根据绝对值的几何意义,得出![]() 的最小值;
的最小值;
(3)根据绝对值的几何意义,得出![]() 的最小值及x的值;
的最小值及x的值;
拓展推广:根据绝对值的几何意义,可得![]() 取最小值时,x的取值为-2≤x≤1;
取最小值时,x的取值为-2≤x≤1;
(4)根据![]() 变形得
变形得![]() ,根据题意及绝对值的几何含义得到x,y的取值即可求解;
,根据题意及绝对值的几何含义得到x,y的取值即可求解;
(5)根据题意分a>0和a<-1两种情况分别求解即可.
(1)解![]()
x+2=1或x+2=-1
解得x=-1或x=-3
(2)根据绝对值的几何意义可得,当2≤x≤6时,![]() 的最小值是8
的最小值是8
故答案为:8;
(3)根据绝对值的几何意义可得,当x=0时,![]() 的最小值是5,
的最小值是5,
故答案为:5; 0;
拓展推广:根据绝对值的几何意义可得:当![]() 的最小值是3时,x的取值为-2≤x≤1
的最小值是3时,x的取值为-2≤x≤1
故答案为:-2≤x≤1;
(4)∵![]()
∴![]()
∵![]() 的最小值为10,
的最小值为10,![]() 的最小值为7,
的最小值为7,
根据绝对值的几何含义可得x的取值是-8≤x≤2;y的取值是-1≤x≤6
故当x=-8,y=-1时![]() 的最小值是-9;
的最小值是-9;
故当x=2,y=6时![]() 的最大值是8;
的最大值是8;
故答案为:-9;8;
(5)如图,当a>0时,∵![]() 的最小值是4.5
的最小值是4.5
∴a=4.5-1=3.5,此时x=0
当a<-1时,∵![]() 的最小值是4.5
的最小值是4.5
∴a=0-4.5=-4.5, 此时x=-1.
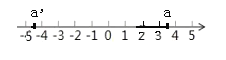

 名校课堂系列答案
名校课堂系列答案