题目内容
【题目】如图,在△ABC中,∠A=70°,∠B=90°,点A关于BC的对称点是A',点B关于AC的对称点是B',点C关于AB的对称点是C',若△ABC的面积是1,则△A'B'C'的面积是( )

A.2B.3C.4D.5
【答案】B
【解析】
BB′的延长线交A′C′于E,如图,根据轴对称的性质得到DB′=DB,BB′⊥AC,BC=BC′,AB=A′B,则可判断△ABC≌△A′BC′,所以∠C=∠A′C′B,AC=A′C′,则AC∥A′C′,所以DE⊥A′C′,且BD=BE,即B′E=3BD,然后利用三角形面积公式可得到S△A′B′C′=3S△ABC.
BB′的延长线交A′C′于E,如图,
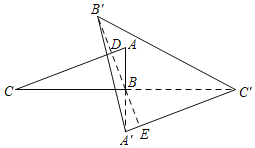
∵点B关于AC的对称点是B',
∴DB′=DB,BB′⊥AC,
∵点C关于AB的对称点是C',
∴BC=BC′,
∵点A关于BC的对称点是A',
∴AB=A′B,
而∠ABC=∠A′BC′,
∴△ABC≌△A′BC′(SAS),
∴∠C=∠A′C′B,AC=A′C′,
∴AC∥A′C′,
∴DE⊥A′C′,
而△ABC≌△A′BC′,
∴BD=BE,
∴B′E=3BD,
∴S△A′B′C′=![]() A′C′×B′E=3×
A′C′×B′E=3×![]() ×BD×AC=3S△ABC=3×1=3.
×BD×AC=3S△ABC=3×1=3.
故选:B.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目




