题目内容
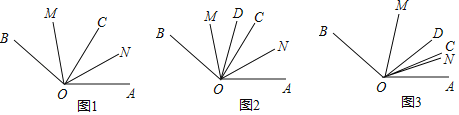
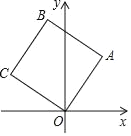
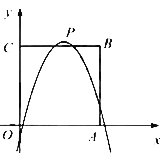
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上,横、纵坐标均为整数的点称为好点.点P为抛物线![]() 的顶点.
的顶点.
(1)当![]() 时,求该抛物线下方(包括边界)的好点个数.
时,求该抛物线下方(包括边界)的好点个数.
(2)当![]() 时,求该抛物线上的好点坐标.
时,求该抛物线上的好点坐标.
(3)若点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点,求m的取值范围.
【答案】(1)好点有:![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,共5个;(2)
,共5个;(2)![]() ,
,![]() 和
和![]() ;(3)
;(3)![]() .
.
【解析】
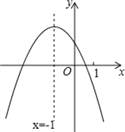
(1)如图1中,当m=0时,二次函数的表达式y=﹣x2+2,画出函数图象,利用图象法解决问题即可;(2)如图2中,当m=3时,二次函数解析式为y=﹣(x﹣3)2+5,如图2,结合图象即可解决问题;(3)如图3中,抛物线的顶点P(m,m+2),推出抛物线的顶点P在直线y=x+2上,由点P在正方形内部,则0<m<2,如图3中,E(2,1),F(2,2),观察图象可知,当点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点时,抛物线与线段EF有交点(点F除外),求出抛物线经过点E或点F时Dm的值,即可判断.
解:(1)当![]() 时,二次函数的表达式为
时,二次函数的表达式为![]()
画出函数图像(图1)
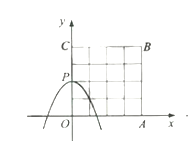
图1
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 抛物线经过点
抛物线经过点![]() 和
和![]()
![]() 好点有:
好点有:![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,共5个
,共5个
(2)当![]() 时,二次函数的表达式为
时,二次函数的表达式为![]()
画出函数图像(图2)
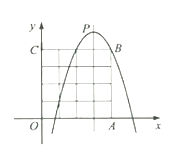
图2
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 该抛物线上存在好点,坐标分别是
该抛物线上存在好点,坐标分别是![]() ,
,![]() 和
和![]()
(3)![]() 抛物线顶点P的坐标为
抛物线顶点P的坐标为![]()
![]() 点P支直线
点P支直线![]() 上
上
由于点P在正方形内部,则![]()
如图3,点![]() ,
,![]()
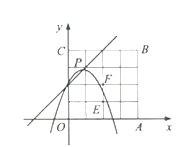
图3
![]() 当顶点P支正方形OABC内,且好点恰好存在8个时,抛物线与线段EF有交点(点F除外)
当顶点P支正方形OABC内,且好点恰好存在8个时,抛物线与线段EF有交点(点F除外)
当抛物线经过点![]() 时,
时,![]()
解得:![]() ,
,![]() (舍去)
(舍去)
当抛物线经过点![]() 时,
时,![]()
解得:![]() ,
,![]() (舍去)
(舍去)
![]() 当
当![]() 时,顶点P在正方形OABC内,恰好存在8个好点
时,顶点P在正方形OABC内,恰好存在8个好点

【题目】某校七年级组织知识竞赛,共设20道选择题,各题分值相同,每题必答.右表记录了5个参赛学生的得分情况.问:
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
D | 14 | 6 | 64 |
E | 10 | 10 | 40 |
(1)答对一题得 分,答错一题得 分;
(2)有一同学说:同学甲得了70分,同学乙得了90分,你认为谁的成绩是准确的?为什么?