题目内容
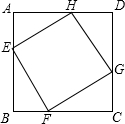
正方形ABCD的边长为1,E、F两点分别位于BC、CD上,DF=m,BE=n,∠EAF=45°,△EFC的内切圆的半径为r.(1)证明:EF=m+n;
(2)证明:(m+1)(n+1)=2;
(3)若m<n,r=
 求m、n的值.
求m、n的值.
【答案】分析:(1)作出辅助线,证出△AGB≌△AFD,根据全等三角形的性质求出AG=AF,∠GAB=∠FAD,再进一步证出
再证出△EAG≌△EAF,得到EG=EF,然后即可求出EF的长.
(2)找到Rt△FEC,将各边用含m的代数式表示,利用勾股定理解答.
(3)根据三角形的面积相等列出关于m、n的等式,结合(2)的结论,即可求出m、n的值.
解答: (1)证明:延长CB至G,使BG=DF,连接AG.
(1)证明:延长CB至G,使BG=DF,连接AG.
在△AGB和△AFD中,
∵AB=AD,∠ABG=∠ADF,BG=DF,
∴△AGB≌△AFD,
∴AG=AF,∠GAB=∠FAD,
又∵∠EAF=45°,
∴∠BAE+∠FAD=∠BAE+∠GAB=45°,
∴∠EAG=∠EAF=45°,
在△EAG和△EAF中,
∵AE=AE,∠EAG=∠EAF,AG=AF,
∴△EAG≌△EAF,
∴EG=EF,
又∵EG=EB+BG=BE+DF=n+m,
∴EF=m+n.
(2)在Rt△FEC中,
∵EF2=CE2+CF2,
∴(m+n)2=(1-n)2+(1-m)2,
展开整理得mn+m+n=1,
两边同加上1,左边因式分解得(m+1)(n+1)=2.
(3)∵S△EFC= (CE+CF+EF)r,
(CE+CF+EF)r,
∴当r= 时得,
时得, (1-m)(1-n)=
(1-m)(1-n)= [(1-m)+(1-n)+(m+n)]×
[(1-m)+(1-n)+(m+n)]× ,
,
整理得(1-m)(1-n)= ,
,
结合第2问结论:
(m+1)(n+1)=2消元得m= ,n=
,n= ;m=
;m= ,n=
,n= .
.
∵m<n,
∴m= ,n=
,n= .
.
点评:此题是一道圆、正方形和三角形相结合的题目,综合性较强.
(1)解答此小题时,要运用全等三角形的知识;
(2)运用勾股定理是解答此题的关键;
(3)根据三角形的面积不变列出等式是常用的解答此类问题方法.
再证出△EAG≌△EAF,得到EG=EF,然后即可求出EF的长.
(2)找到Rt△FEC,将各边用含m的代数式表示,利用勾股定理解答.
(3)根据三角形的面积相等列出关于m、n的等式,结合(2)的结论,即可求出m、n的值.
解答:
 (1)证明:延长CB至G,使BG=DF,连接AG.
(1)证明:延长CB至G,使BG=DF,连接AG.在△AGB和△AFD中,
∵AB=AD,∠ABG=∠ADF,BG=DF,
∴△AGB≌△AFD,
∴AG=AF,∠GAB=∠FAD,
又∵∠EAF=45°,
∴∠BAE+∠FAD=∠BAE+∠GAB=45°,
∴∠EAG=∠EAF=45°,
在△EAG和△EAF中,
∵AE=AE,∠EAG=∠EAF,AG=AF,
∴△EAG≌△EAF,
∴EG=EF,
又∵EG=EB+BG=BE+DF=n+m,
∴EF=m+n.
(2)在Rt△FEC中,
∵EF2=CE2+CF2,
∴(m+n)2=(1-n)2+(1-m)2,
展开整理得mn+m+n=1,
两边同加上1,左边因式分解得(m+1)(n+1)=2.
(3)∵S△EFC=
 (CE+CF+EF)r,
(CE+CF+EF)r,∴当r=
 时得,
时得, (1-m)(1-n)=
(1-m)(1-n)= [(1-m)+(1-n)+(m+n)]×
[(1-m)+(1-n)+(m+n)]× ,
,整理得(1-m)(1-n)=
 ,
,结合第2问结论:
(m+1)(n+1)=2消元得m=
 ,n=
,n= ;m=
;m= ,n=
,n= .
.∵m<n,
∴m=
 ,n=
,n= .
.点评:此题是一道圆、正方形和三角形相结合的题目,综合性较强.
(1)解答此小题时,要运用全等三角形的知识;
(2)运用勾股定理是解答此题的关键;
(3)根据三角形的面积不变列出等式是常用的解答此类问题方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 附加题
附加题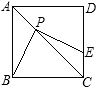 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3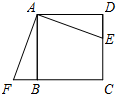 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=