题目内容
正方形ABCD的边长为4,P是BC上一动点,QP⊥AP交DC于Q,设PB=x,△ADQ的面积为y.(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)(1)中函数若是一次函数,求出直线与两坐标轴围成的三角形面积;若是二次函数,请利用配方法求出抛物线的对称轴和顶点坐标;
(3)画出这个函数的图象;
(4)点P是否存在这样的位置,使△APB的面积是△ADQ的面积的
| 2 | 3 |
分析:(1)Rt△ADQ中,已知了直角边AD的长,欲求其面积,需求得直角边DQ的长;已知∠APQ=90°,显然△ABP∽△PCQ,用x表示出BP、CP的长,根据相似三角形所得比例线段,即可求得CQ的表达式,可得到DQ的表达式,从而根据直角三角形的面积公式求出y、x的函数关系式.
(2)由(1)可知,y、x的函数关系式是个二次函数,用配方法将其解析式化为顶点坐标式,即可求得抛物线的顶点坐标和对称轴方程.
(3)可根据(1)所得抛物线的解析式,通过描点、连线画出此抛物线的图象.
(4)由于BP=x,易知△ABP的面积为2x,根据△ABP和△ADQ的面积关系,可得到关于x的方程,通过解方程可求得x的值即BP的长(注意x的值应符合自变量的取值范围),从而确定出点P在线段BC上的位置.
(2)由(1)可知,y、x的函数关系式是个二次函数,用配方法将其解析式化为顶点坐标式,即可求得抛物线的顶点坐标和对称轴方程.
(3)可根据(1)所得抛物线的解析式,通过描点、连线画出此抛物线的图象.
(4)由于BP=x,易知△ABP的面积为2x,根据△ABP和△ADQ的面积关系,可得到关于x的方程,通过解方程可求得x的值即BP的长(注意x的值应符合自变量的取值范围),从而确定出点P在线段BC上的位置.
解答: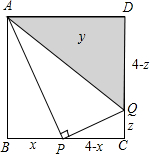 解:(1)画出图形,
解:(1)画出图形,
设QC=z,由Rt△ABP~Rt△PCQ,
=
,
z=
,①
y=
×4×(4-z),②
把①代入②y=
x2-2x+8(0<x<4).
(2)y=
x2-2x+8=
(x-2)2+6,
∴对称轴为x=2,顶点坐标为(2,6).
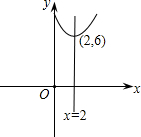
(3)如图所示;
(4)存在,由S△APB=
S△ADQ,可得y=3x,
∴
x2-2x+8=3x,
∴x=2,x=8(舍去),
∴当P为BC的中点时,△PAB的面积等于△ADQ的面积的
.
 解:(1)画出图形,
解:(1)画出图形,设QC=z,由Rt△ABP~Rt△PCQ,
| 4 |
| 4-x |
| x |
| z |
z=
| x(4-x) |
| 4 |
y=
| 1 |
| 2 |
把①代入②y=
| 1 |
| 2 |
(2)y=
| 1 |
| 2 |
| 1 |
| 2 |
∴对称轴为x=2,顶点坐标为(2,6).

(3)如图所示;
(4)存在,由S△APB=
| 2 |
| 3 |
∴
| 1 |
| 2 |
∴x=2,x=8(舍去),
∴当P为BC的中点时,△PAB的面积等于△ADQ的面积的
| 2 |
| 3 |
点评:本题是几何与代数的综合应用,同时也是一道探索性问题.在实际问题中,自变量的取值应结合实际意义确定.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 附加题
附加题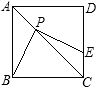 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3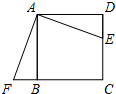 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=