题目内容
(1)点(-1,2)关于直线x=1对称的点的坐标是(2)直线y=2x+4关于直线x=1的对称的直线的解析式是
(3)已知A(5,5),B(2,4)在x轴上是否存在一点M,使MA+MB的值最小?若存在,求出M点的坐标.
分析:(1)点(-1,2)的横坐标为[1-(-1)]×2,纵坐标不变,可得点(-1,2)关于直线x=1对称的点的坐标;
(2)找到直线y=2x+4上的两点,得到它们关于直线x=1的对称点,再用待定系数法求出解析式;
(3)先得到点B(2,4)关于x轴对称的点为B'(2,-4),再用待定系数法求出AB'的解析式,再解出AB'与x轴的交点坐标,从而求解.
(2)找到直线y=2x+4上的两点,得到它们关于直线x=1的对称点,再用待定系数法求出解析式;
(3)先得到点B(2,4)关于x轴对称的点为B'(2,-4),再用待定系数法求出AB'的解析式,再解出AB'与x轴的交点坐标,从而求解.
解答:解:(1)(3,2)…(1分)
(2)y=-2x+8…(2分)
(3)点B(2,4)关于x轴对称的点为B'(2,-4)…(3分)
设AB'的解析式为y=kx+b
则
,
解得
…(4分)
∴y=3x-10
令y=0,则x=
,
∴M(
,0).…(6分)
(2)y=-2x+8…(2分)
(3)点B(2,4)关于x轴对称的点为B'(2,-4)…(3分)
设AB'的解析式为y=kx+b
则
|
解得
|
∴y=3x-10
令y=0,则x=
| 10 |
| 3 |
∴M(
| 10 |
| 3 |
点评:本题考查了坐标与图形变化-对称轴对称-最短路线问题,注意待定系数法求直线解析式的运用,有一定的难度.

练习册系列答案
相关题目
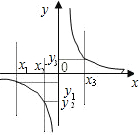 在函数y=
在函数y=| k |
| x |
| A、y1<0<y2 |
| B、y3<0<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
 9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为
9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为 23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.