题目内容
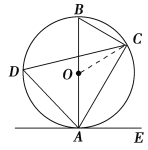
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°。
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧![]() 的长。(本题12分)
的长。(本题12分)

【答案】(1)、60°;(2)、证明过程见解析;(3)、![]() π
π
【解析】
试题分析:(1)、根据同弧所对的圆周角相等得出答案;(2)、根据直径得出∠BAC=30°,从而得出∠BAE=90°,然后得出切线;(3)、连接OC,从而得出△OBC为等边三角形,然后得出∠AOC=120°,最后根据弧长的计算公式得出答案.
试题解析:(1)、∵∠ABC与∠D都是![]() 所对的圆周角,∴∠ABC=∠D=60°.
所对的圆周角,∴∠ABC=∠D=60°.
(2)、∵AB是⊙O的直径, ∴∠ACB=90°, ∴∠BAC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°, 即BA⊥AE,∴AE是⊙O的切线.
(3)、如图,连接OC. ∵OB=OC,∠ABC=60°, ∴△OBC是等边三角形,
∴OB=BC=4,∠BOC=60°, ∴∠AOC=120°. ∴![]() 的长度为=
的长度为=![]() =
=![]() π.
π.

练习册系列答案
相关题目