Question

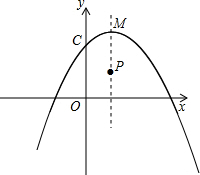如图，抛物线y=ax²+bx+c的顶点M的坐标是（1，3），且与y轴相交于点C（0，2），P（1，1）是抛物线对称轴上的一点．请回答下列问题：
（1）写出抛物线的解析式

 

；
（2）点Q是抛物线上的一点，且使△CPQ的面积等于△CMP的面积，则所有满足条件的点Q的个数为：

 

．

Answer 1

分析：（1）设抛物线的解析式为y=a（x-1）²+3，然后把C（0，2）代入计算出a的值即可；
（2）通过△CPQ的面积等于△CMP的面积可得点Q在与PC平行且到CP的距离等于点M到CP的距离的两条平行直线上，先利用待定系数法确定直线PC的解析式为y=-x+2，
根据两直线平行则k相等得到直线MQ₁的解析式为y=-x+4，把M（1，3）代入确定直线MQ₁的解析式为y=-x+4，然后把y=-x²+2x+2和y=-x+4联立起来解方程组即可得到它们交点的坐标，即得到Q₁的坐标；再直线MQ₁向下平移4个单位后与PC的距离不变，此时平移后的直线的解析式为y=-x，利用同样的方法可求出直线y=-x与抛物线的交点坐标即Q₂的坐标，Q₃的坐标．

解答：解：（1）设抛物线的解析式为y=a（x-1）²+3，
把C（0，2）代入得，a+3=2，解得a=-1，
∴抛物线的解析式为y=-（x-1）²+3=-x²+2x+2．
故答案为y=-x²+2x+2．

（2）∵△CPQ的面积等于△CMP的面积，
∴点Q到CP的距离等于点M到CP的距离，即点Q在与PC平行且到CP的距离等于点M到CP的距离的两条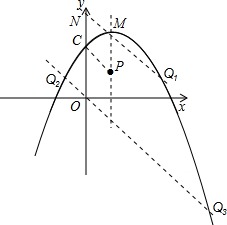平行直线上，如图，
设直线PC的解析式为y=kx+b，
把C（0，2），P（1，1）代入得，k+2=1，b=2，解得k=-1，
∴直线PC的解析式为y=-x+2，
又∵MQ₁∥PC，
∴设直线MQ₁的解析式为y=-x+b，
把M（1，3）代入得b=4，
∴直线MQ₁的解析式为y=-x+4，
联立

y=-x2+2x+2 y=-x+4

，解得

x1=1 y 1=3

，

x2=2 y2=2

，
∴Q₁的坐标为（2，2）；
直线MQ₁y=-x+4与y轴的交点N的坐标为（0，4），所以把直线MQ₁向下平移4个单位后与PC的距离不变，此时平移后的直线的解析式为y=-x，设它与抛物线的交
点为Q₂，Q₃，如图，
联立

y=-x2+2x+2 y=-x

，解得

x 1= 3+ 17 2 y1= -3- 17 2

，

x2= 3- 17 2 y2= -3+ 17 2

，
∴Q₂的坐标为（

3- 17

2

，

-3+ 17

2

），Q₃的坐标为（

3+ 17

2

，

-3- 17

2

）；
所以满足条件的点Q的个数有三个．
故答案为y=-x²+2x+2；3．

点评：本题考查了解二次函数综合题的方法：先合理设解析式，再利用待定系数法确定解析式，然后利用二次函数的图象和性质解决其他问题．也考查了两直线平行k相等的性质以及把求两函数图象的交点坐标转化为解方程组的问题．