��Ŀ����
����Ŀ��ѧУ��ѧ��ȤС�����û����˿�չ��ѧ��������![]() ����λ���ȵ�ֱ���ܵ�
����λ���ȵ�ֱ���ܵ�![]() �ϣ������˼״Ӷ˵�
�ϣ������˼״Ӷ˵�![]() ���������������ڶ˵�
���������������ڶ˵�![]() ��
��![]() ֮�䣬��������ͬʱ�Ӷ˵�
֮�䣬��������ͬʱ�Ӷ˵�![]() �������Դ��ڼ��ٶ����������ڶ˵�
�������Դ��ڼ��ٶ����������ڶ˵�![]() ��
��![]() ֮�䣮���ǵ���˵������ת���۷�����ʱ���Բ��ƣ���ȤС���Ա̽��������������ӭ�����������������ġ�ӭ������������������������ڶ˵㴦���������֣�
֮�䣮���ǵ���˵������ת���۷�����ʱ���Բ��ƣ���ȤС���Ա̽��������������ӭ�����������������ġ�ӭ������������������������ڶ˵㴦���������֣�
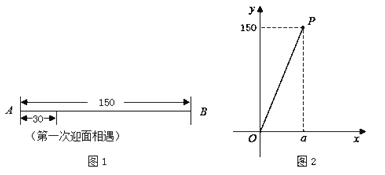
���۲죩
�ٹ۲�ͼ![]() ���������������˵�һ��ӭ������ʱ�������ص����
���������������˵�һ��ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ������ǵڶ���ӭ������ʱ�������ص����
����λ���ȣ������ǵڶ���ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ _____����λ���ȣ�
֮��ľ���Ϊ _____����λ���ȣ�
���������������˵�һ��ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ������ǵڶ���ӭ������ʱ�������ص����
����λ���ȣ������ǵڶ���ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ _____����λ���ȣ�
֮��ľ���Ϊ _____����λ���ȣ�
�����֣�
�������������˵�һ��ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ����ǵڶ���ӭ������ʱ�������ص����
����λ���ȣ����ǵڶ���ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ���ȤС���Ա������
����λ���ȣ���ȤС���Ա������![]() ��
��![]() �ĺ�����ϵ���������˲��ֺ���ͼ���߶�
�ĺ�����ϵ���������˲��ֺ���ͼ���߶�![]() ����������
����������![]() ����ͼ
����ͼ![]() ��ʾ����
��ʾ����
��![]() �� _____��
�� _____��
�ڷֱ����������ͼ���Ӧ�ĺ�������ʽ������ͼ![]() �в�ȫ����ͼ��
�в�ȫ����ͼ��
����չ��
�������������˵�һ��ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ����ǵ�����ӭ������ʱ�������ص����
����λ���ȣ����ǵ�����ӭ������ʱ�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ��������������˵�����ӭ������ʱ�������ص����
����λ���ȣ��������������˵�����ӭ������ʱ�������ص����![]() ֮��ľ���
֮��ľ���![]() ������
������![]() ����λ���ȣ������ǵ�һ��ӭ������ʱ�������ص����
����λ���ȣ������ǵ�һ��ӭ������ʱ�������ص����![]() ֮��ľ���
֮��ľ���![]() ��ȡֵ��Χ�� _____����ֱ��д�������
��ȡֵ��Χ�� _____����ֱ��д�������
���𰸡����۲졿����![]() ����
����![]() �������֡�����
�������֡�����![]() ���ڼ�����������չ����0��x��12��48��x��72��
���ڼ�����������չ����0��x��12��48��x��72��
��������
[�۲�]�����ʱ��������AΪm����λ�����������з��̼��ɵõ����ۣ�
�ڴ�ʱ��������AΪm����λ�����������з��̼��ɵõ����ۣ�
[����]�ٵ���ڶ��������ص�պ��ڵ�Bʱ��������˼��ٶ�Ϊv����������ҵ��ٶ�Ϊ![]() �����������з��̼��ɵõ����ۣ�
�����������з��̼��ɵõ����ۣ�
��������˼��ٶ�Ϊv����������ҵ��ٶ�Ϊ![]() �����������к�������ʽ���ɵõ����ۣ�
�����������к�������ʽ���ɵõ����ۣ�
[��չ]�������в���ʽ���ɵõ����ۣ�
[�۲�]�١������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ�
����λ���ȣ�
�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ�
����λ���ȣ�
������˼��ٶ�Ϊ![]() ��
��
��������ҵ��ٶ�Ϊ![]() ��
��
������˼״������㵽��B���õ�ʱ��Ϊ![]() ��
��
�������Ҵ������ص㵽��![]() �ٷ��ص���
�ٷ��ص���![]() ����ʱ��Ϊ
����ʱ��Ϊ![]() ����
����![]() ��
��
��������˼���������ҵڶ���ӭ������ʱ��
�������Ҵӵ�һ�������ص㵽��![]() �����ص���
�����ص���![]() ���ٷ�����
���ٷ�����![]() ʱ�ͻ����˼ڶ���ӭ��������
ʱ�ͻ����˼ڶ���ӭ��������
���ʱ��������![]() Ϊ
Ϊ![]() ����λ��
�����
��������ã�![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��
![]()
�ڡ������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ�
����λ���ȣ�
�������ص����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����λ���ȣ�
����λ���ȣ�
������˼��ٶ�Ϊ![]() ��
��
��������ҵ��ٶ�Ϊ![]() ��
��
��������Ҵ������㵽��![]() �ٵ���
�ٵ���![]() ���õ�ʱ��Ϊ
���õ�ʱ��Ϊ ��
��
�����˼״������㵽��![]() ����ʱ��Ϊ
����ʱ��Ϊ![]() ����
����![]() ��
��
��������˼���������ҵڶ���ӭ������ʱ�������˴ӵ�һ�������㵽��![]() ���ٵ���
���ٵ���![]() ������ʱ�ͻ������ҵڶ���ӭ��������
������ʱ�ͻ������ҵڶ���ӭ��������
���ʱ��������![]() Ϊ
Ϊ![]() ����λ��
�����
��������ã�![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��
[����]�ٵ���ڶ��������ص�պ��ڵ�![]() ʱ��
ʱ��
������˼��ٶ�Ϊ![]() ����������ҵ��ٶ�Ϊ
����������ҵ��ٶ�Ϊ![]() ��
��
��������֪��![]() ��
��
![]() ��
��
�����飺![]() �Ƿ�ʽ���̵ĸ���
�Ƿ�ʽ���̵ĸ���
����![]() ��
��
�ʴ�Ϊ��![]() ��
��
�ڵ�![]() ʱ����
ʱ����![]() ���߶�
���߶�![]() �ϣ�
�ϣ�
���߶�![]() �ı���ʽΪ
�ı���ʽΪ![]() ��
��
��![]() ʱ������
ʱ������![]() ����ʱ���ڶ��������ص��ǻ����˼��ڵ���
����ʱ���ڶ��������ص��ǻ����˼��ڵ���![]() �������
�������![]() ʱ��
ʱ��
������˼��ٶ�Ϊ![]() ����������ҵ��ٶ�Ϊ
����������ҵ��ٶ�Ϊ![]() ��
��
��������֪��![]() ��
��
![]() ��
��
����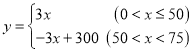 ��
��
��ȫͼ����ͼ2��ʾ��

[��չ]����ͼ��
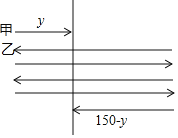
������֪��![]() ��
��
��y=5x��
��0��y��60��
��0��x��12��
����ͼ��

��![]() ��
��
��y=-5x+300��
��0��y��60��
��48��x��60��
����ͼ��

������ã�![]() ��
��
��y=5x-300��
��0��y��60��
��60��x��72��
��0��x��75��
��48��x��72��
���������������ص����A֮��ľ���x��ȡֵ��Χ��0��x��12��48��x��72��
�ʴ�Ϊ0��x��12��48��x��72��

����Ŀ�������������־��á��ǻ����һ�����ָ����������ݴ�ؼ������ڵڶ��������й��������ٿ�֮�ʣ�ijУ�����˵ڶ����������¼������߽���ʱ������Ϣ����Ӧ�ô���������У���꼶�μӾ�����ѧ���ɼ�ͳ�ƺ��Ƴ�����ͳ��ͼ��������������
�������¼������߽���ʱ������Ϣ����Ӧ�ô����ɼ�Ƶ���ֲ�ͳ�Ʊ�
��� | �ɼ�x���֣� | ���� |
A | 60��x��70 | 10 |
B | 70��x��80 | m |
C | 80��x��90 | 16 |
D | 90��x��100 | 4 |
��۲������ͼ��������������⣺
��1��ͳ�Ʊ���m���� ����ͳ��ͼ��n���� ����D���Բ�Ľ����� ���ȣ�
��2��D���4��ѧ���У���2��������2��Ů������D�������ȡ2��ѧ���μ�5G���������㻭����״ͼ�����б�����
��ǡ��1��������1��Ů������ȡ�μ�5G�����ĸ��ʣ�
������1��Ů������ȡ�μ�5G�����ĸ��ʣ�

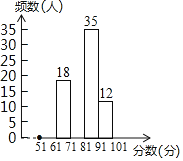
����Ŀ��Ϊ����ǿѧ���İ�ȫ��ʶ��ijУ��֯��һ��ȫУ2500��ѧ�����μӵġ���ȫ֪ʶ�����ԣ��ľ���ѧУ��ί�����ȡ��100�ݿ������з���ͳ�ƣ����ֿ��Գɼ���![]() �֣�����ͷ�Ϊ51�֣���߷�Ϊ����100�֣��������������в�������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺
�֣�����ͷ�Ϊ51�֣���߷�Ϊ����100�֣��������������в�������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺
�����Σ��֣� | Ƶ�����ˣ� | Ƶ�� |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
�ϼ� | 100 | 1 |
��1����գ�![]() ______��
______��![]() ______��
______��![]() ______��
______��
��2����Ƶ���ֲ�ֱ��ͼ����������
��3����У�Կ��Գɼ�Ϊ![]() ��ѧ�����н��������ɼ��Ӹ߷ֵ��ͷ���һ���������Ƚ�������һ���������Ƚ�����������Ϊ1��3��6���������ȫУ��ö��Ƚ���ѧ������.
��ѧ�����н��������ɼ��Ӹ߷ֵ��ͷ���һ���������Ƚ�������һ���������Ƚ�����������Ϊ1��3��6���������ȫУ��ö��Ƚ���ѧ������.