题目内容
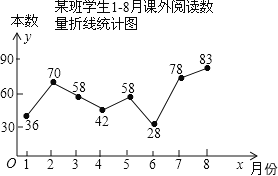
【题目】为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(![]() 分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
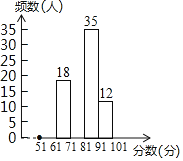
分数段(分) | 频数(人) | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为![]() 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.
的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.
【答案】(1)10 ,25 , 0.25;见解析;(3)全校获得二等奖的学生人数90人.
【解析】
(1)利用×这组的频率即可得到结论;
(2)根据(1)求出的数据补全频数分布直方图即可;
(3)利用全校2500名学生数×考试成绩为![]() 考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论.
考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论.
解:(1)![]() ,
,![]() ,
,![]() ;
;
故答案为:10,25,0.25;
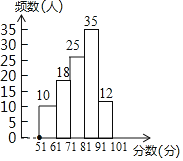
(2)补全频数分布直方图如图所示;
(3)![]() (人),
(人),
答:全校获得二等奖的学生人数90人.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期 | 29日 | 30日 | 5月1日 | 2日 | 3日 | 4日 | 5日 |
日最高气温 | 16°C | 19°C | 22°C | 24°C | 26°C | 24°C | 23°C |
A. 24,23,10B. 24,23,![]() C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,![]()