题目内容
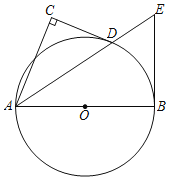
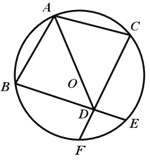
【题目】已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.
(1)求证:BD=CD:
(2)如果AB2=AO·AD,求证:四边形ABDC是菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接BC,根据垂直平分线的性质即可解答
(2)连接OB,先求出△ABO∽△ADB,再利用相似的性质,求出四边形ABDC的四边相等,即可解答
(1)连接BC,

在⊙O中,∵AB=AC,∴△ABC为等腰三角形
又∵AD经过圆心O,∴AD垂直平分BC ∴BD=CD.
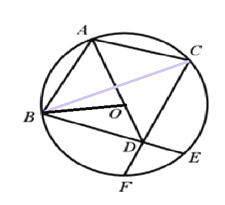
(2)连接OB.
∵AB2=AO·AD,![]()
又∵∠BAO=∠DAB,
∴△ABO∽△ADB
∴∠OBA=∠BDA
∵OA=OB,
∴∠OBA=∠OAB.
∴∠OAB=∠BDA
∴AB=BD.
又∵AB=AC,BD=CD,
∴AB=AC=BD=CD.
∴四边形ABDC是菱形.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目