题目内容
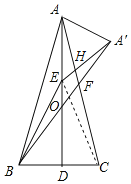
【题目】如图，AD是△ABC的高线，BD＝CD，点E是AD上一点，BE＝BC，将△ABE沿BE所在直线折叠，点A落在点A′位置上，连接AA'，BA′，EA′与AC相交于点H，BA′与AC相交于点F．小夏依据上述条件，写出下列四个结论：①∠EBC＝60°；②∠BFC＝60°；③∠EA′A＝60°；④∠A′HA＝60°.以上结论中，正确的是（ ）
A.①B.③④C.①②③D.①②④
【答案】C
【解析】
连接EC，设AD与BA'相交于点O，如图，由线段垂直平分线的性质可证△BEC是等边三角形，进一步可得∠EBC＝∠BEC＝∠BCE＝60°，∠BED＝∠CED＝30°，进而可判断①；由折叠的性质可得∠AEB＝∠BEA'＝150°，继而可得∠AEA'＝60°，于是可证△AEA'是等边三角形，进而可判断③；由“SSS”可证△ABE≌△ACE，可得∠BAD＝∠DAC＝∠BA'E，进一步由三角形的外角性质可得∠EOA'+∠CAD＝∠BFC＝60°，进而可判断②；由∠A'HA＝∠AEA'+∠EAH＞60°，可对④进行判断．
解：连接EC，设AD与BA'相交于点O，如图，
∵BD＝CD，AD⊥BC，∴AD垂直平分BC，∴BE＝EC，
∵BE＝BC，∴BE＝EC＝BC，
∴△BEC是等边三角形，且ED⊥BC，
∴∠EBC＝∠BEC＝∠BCE＝60°，∠BED＝∠CED＝30°，故结论①正确；
∴∠AEB＝150°，
∵将△ABE沿BE所在直线折叠，点A落在点A′位置，
∴∠AEB＝∠BEA'＝150°，AE＝A'E，∠BAD＝∠BA'E，
∴∠AEA'＝60°，
∴△AEA'是等边三角形，∴∠EA'A＝60°，故结论③正确；
∵AB＝AC，BE＝EC，AE＝AE，
∴△ABE≌△ACE（SSS），
∴∠BAD＝∠DAC＝∠BA'E，
∵∠AEA'＝∠EOA'+∠EA'O＝60°，
∴∠EOA'+∠CAD＝∠BFC＝60°，故结论②正确；
∵∠A'HA＝∠AEA'+∠EAH＞60°，∴结论④错误.
故选：C．
