��Ŀ����
����Ŀ����ͼ����֪Rt��ABC�У���C��90����AC��8��BC��6����P��ÿ��1����λ���ٶȴ�A��C�˶���ͬʱ��Q��ÿ��2����λ���ٶȴ�A��B��C�����˶������ǵ�C���ֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
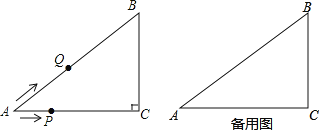
��1����t��2.5ʱ��PQ���� ����
��2������t����˶�������ABC��ֱ��PQɨ�������S��ʱ��t�ĺ�����ϵʽ��
��3��P��Q�������˶������У��Ƿ����ʱ��t��ʹ����PQCΪ���������Σ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��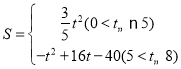 ��3�����ڣ���t��
��3�����ڣ���t��![]() ��t��
��t��![]() ��t��3.4ʱ����PQCΪ���������Σ�
��t��3.4ʱ����PQCΪ���������Σ�
��������
��1����ͼ1����Q��QE��AC��E������PQ�����QE��PE�����ù��ɶ������ɽ�����⣮
��2���������ε������ʽ������ã�
��3�����ڣ���ͼ2������CQ��PQ������������ٵ�CQ=CPʱ���ڵ�PQ=CQʱ���۵�PQ=PCʱ���з�����⼴�ɣ�
��1����ͼ1����Q��QE��AC��E������PQ��
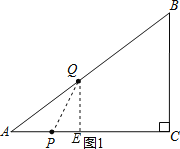
��Rt��ABC�У��ߡ�C��90����AC��8��BC��6��
��AB��![]() ��10��
��10��
��t��2.5��
��AQ��5��AP��2.5��
��QE��BC��
![]() ,
,
![]() ,
,
��QE��3��AE��4��
��PE��4��2.5��1.5��
��PQ��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ1����ABC��ֱ��PQɨ���������S��AQP��
��Q��AB����ʱ��S��![]() ����0��t��5��
����0��t��5��
��Q��BC����ʱ����ABC��ֱ��PQɨ���������S�ı���ABQP��
��S�ı���ABQP��S��ABC��S��PQC��![]() ��8��6��
��8��6��![]() ��8��t����16��2t������t2+16t��40����5��t��8����
��8��t����16��2t������t2+16t��40����5��t��8����
�ྭ��t����˶�����ABC��ֱ��PQɨ�������S��ʱ��t�ĺ�����ϵʽ�ǣ�
S��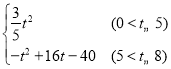 ��
��
��3�����ڣ�
����Q��AB����ʱ����ͼ2������CQ��PQ��
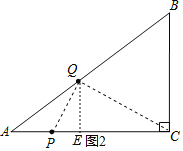
�ɣ�1��֪QE��![]() t��CE��AC��AE��8��
t��CE��AC��AE��8��![]() t��PQ��
t��PQ��![]() t��
t��
��CQ��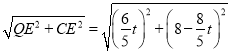 ��
��
�ٵ�CQ��CPʱ��
����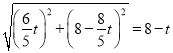 ��
��
��ã�t��![]() ��
��
�ڵ�PQ��CQʱ��
����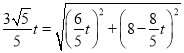 ��
��
��ã�t��![]() ��8������������ȥ����
��8������������ȥ����
�۵�PQ��PCʱ��
����![]() t��8��t��
t��8��t��
��ã�t��3.4��
����Q��BC����ʱ��
�ߡ�ACB��90����
���PQC�ǵ���ֱ�������Σ�
��CQ��CP��
��8��t��16��2t��
��t��8����P��Q��C�غϣ��������⣬
������������t��![]() ��t��
��t��![]() ��t��3.4ʱ����PQCΪ���������Σ�
��t��3.4ʱ����PQCΪ���������Σ�

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�����Ŀ��ijũ��������ͬ��������ij���������ӷ�ѿ�ʵ����飬������±���ʾ��
���Ӹ���n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
��ѿ���Ӹ���m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
��ѿ����Ƶ�� | 0��899 | 0��910 | 0��898 | 0��911 | 0��909 | 0��912 | 0��908 | 0��910 |
һ��أ�![]() �������������д�Լ�ж����Dz��ܷ�ѿ�ģ�
�������������д�Լ�ж����Dz��ܷ�ѿ�ģ�