题目内容
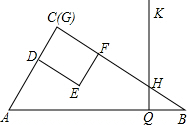如图，在Rt△ABC中，∠C=90°，AB=50，AC=30，矩形DEFG的顶点G与△ABC的顶点C重合，边GD、GF分别与AC，BC重合．GD=12，GF=16，矩形DEFG沿射线CB的方向以每秒4个单位长的速度匀速运动，点Q从点B出发沿BA方向以每秒5个单位长的速度匀速运动，过点Q作射线QK⊥AB，交折线BC-CA于点H，矩形DEFG、点Q同时出发，当点Q到达点A时停止运动，矩形DEFG也随之停止运动．设矩形DEFG、点Q运动的时间是t秒（t＞0）．（1）求线段DF的长；
（2）求运动过程中，矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式（写出自变量的取值范围）；
（3）射线QK能否把矩形DEFG分成面积相等的两部分？若能，求出t值；若不能，说明理由；
（4）连接DH，当DH∥AB时，请直接写出t值．
分析：（1）连接DF，在Rt△CDF中，根据勾股定理可得DF的长；
（2）分①当0＜t≤2时；②当2＜t≤6时；③当6＜t≤10时三种情况讨论得到矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式；
（3）当QK经过矩形DEFG的对称中心O时，就可以把矩形DEFG分成面积相等的两部分；易得∠GFD=∠B，可得DF∥AB，然后根据平行线分线段成比例定理求出t值；
（4）由于当DH∥AB，可知D、H的纵坐标相等，依此可得关于t的方程，求出t值即可．
（2）分①当0＜t≤2时；②当2＜t≤6时；③当6＜t≤10时三种情况讨论得到矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式；
（3）当QK经过矩形DEFG的对称中心O时，就可以把矩形DEFG分成面积相等的两部分；易得∠GFD=∠B，可得DF∥AB，然后根据平行线分线段成比例定理求出t值；
（4）由于当DH∥AB，可知D、H的纵坐标相等，依此可得关于t的方程，求出t值即可．
解答：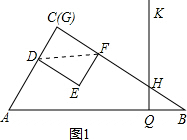
解：（1）如图1：连接DF，在Rt△CDF中，CD=12，CF=16，
根据勾股定理：
DF=
=20；
（2）∵在Rt△ABC中，∠C=90°，AB=50，AC=30，
∴BC=
=40，
根据题意得：当t=
=10时，停止运动；
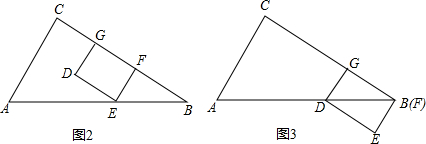如图2：当点E在AB上时，
∵∠C=90°，∠EFG=90°，
∴EF∥AC，
∴△BEF∽△BAC，
∴EF：AC=BF：BC，
∴12：30=BF：40，
∴BF=16，
∴CG=BC-BF-GF=40-16-16=8，
此时，t=8÷4=2；
如图3：当F与B重合时，
CG=BC-BG=40-16=24，
此时，t=24÷4=6，
∵tan∠ABC=
=
，tan∠GBD=
=
，
∴此时，点D在直线AB上；
①当0＜t≤2时，s=S矩形DEFG=12×16=192，
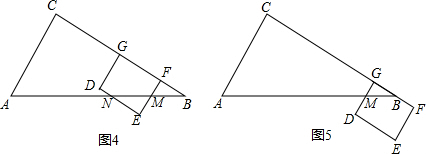
②如图4：当2＜t≤6时，设矩形DEFG的边EF交BC于点M，边DE交AB于点N
∵BF=24-4t tanB=
=
∴MF=
（24-4t）=18-3t，
∴EM=EF-FM=12-（18-3t）=3t-6，
∴NE=
EM=4t-8，
∴s=S矩形DEFG-S△EMN=192-
EM•EN=192-6（t-2）2，
③如图5：当6＜t≤10时，设DG与AB交于点M，BG=40-4t，
则MG=
BG=30-3t，
则s=S△BMG=
BG•MG=
×（40-4t）（30-3t）=6（10-t）2；
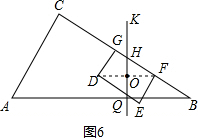（3）能，
如图6：当QK经过矩形DEFG的对称中心O时，就可以把矩形DEFG分成面积相等的两部分；
∵在Rt△GDF与Rt△CAB中，tan∠GDF=
=
=
，tan∠B=
=
，
∴∠GFD=∠B，
∴DF∥AB，
∴
=
，
∵DF=20，
∴OF=10，
∵BF=24-4t，HF=
OF=
，QB=5t，
∴BH=BF+FH=24-4t+
，
∴
=
，
解得：t=
；
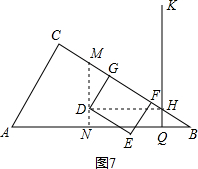（4）如图7：过点D作MN⊥AB于N，交BC于M，
∵∠GMD+∠B=90°，∠GMD+∠GDM=90°，
∴∠GDM=∠B，
∴GM=GD•tan∠GDM=
×12=9，
∴DM=
=15，
∵BG=40-4t，
∴BM=BG+GM=40-4t+9=49-4t，
∴MN=BM•cos∠B=
（49-4t），
∴DN=MN-DM=
（49-4t）-15，
∵QH=
QB=
×5t=
t，
∵DH∥AB，
∴QH=DN，
则
t=
（49-4t）-15，
解得t=
．
故t值为
．
解：（1）如图1：连接DF，在Rt△CDF中，CD=12，CF=16，根据勾股定理：
DF=
| 122+162 |
（2）∵在Rt△ABC中，∠C=90°，AB=50，AC=30，
∴BC=
| AB2-AC2 |
根据题意得：当t=
| 50 |
| 5 |
如图2：当点E在AB上时，∵∠C=90°，∠EFG=90°，
∴EF∥AC，
∴△BEF∽△BAC，
∴EF：AC=BF：BC，
∴12：30=BF：40，
∴BF=16，
∴CG=BC-BF-GF=40-16-16=8，
此时，t=8÷4=2；
如图3：当F与B重合时，
CG=BC-BG=40-16=24，
此时，t=24÷4=6，
∵tan∠ABC=
| AC |
| BC |
| 3 |
| 4 |
| GD |
| BG |
| 3 |
| 4 |
∴此时，点D在直线AB上；
①当0＜t≤2时，s=S矩形DEFG=12×16=192，②如图4：当2＜t≤6时，设矩形DEFG的边EF交BC于点M，边DE交AB于点N
∵BF=24-4t tanB=
| 30 |
| 40 |
| 3 |
| 4 |
∴MF=
| 3 |
| 4 |
∴EM=EF-FM=12-（18-3t）=3t-6，
∴NE=
| 4 |
| 3 |
∴s=S矩形DEFG-S△EMN=192-
| 1 |
| 2 |
③如图5：当6＜t≤10时，设DG与AB交于点M，BG=40-4t，
则MG=
| 3 |
| 4 |
则s=S△BMG=
| 1 |
| 2 |
| 1 |
| 2 |
（3）能，如图6：当QK经过矩形DEFG的对称中心O时，就可以把矩形DEFG分成面积相等的两部分；
∵在Rt△GDF与Rt△CAB中，tan∠GDF=
| DG |
| GF |
| 12 |
| 16 |
| 3 |
| 4 |
| AC |
| BC |
| 3 |
| 4 |
∴∠GFD=∠B，
∴DF∥AB，
∴
| OF |
| QB |
| HF |
| BH |
∵DF=20，
∴OF=10，
∵BF=24-4t，HF=
| 5 |
| 4 |
| 25 |
| 2 |
∴BH=BF+FH=24-4t+
| 25 |
| 2 |
∴
| 10 |
| 5t |
| ||
24-4t+
|
解得：t=
| 146 |
| 41 |
（4）如图7：过点D作MN⊥AB于N，交BC于M，∵∠GMD+∠B=90°，∠GMD+∠GDM=90°，
∴∠GDM=∠B，
∴GM=GD•tan∠GDM=
| 3 |
| 4 |
∴DM=
| DG2+GM2 |
∵BG=40-4t，
∴BM=BG+GM=40-4t+9=49-4t，
∴MN=BM•cos∠B=
| 3 |
| 5 |
∴DN=MN-DM=
| 3 |
| 5 |
∵QH=
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 4 |
∵DH∥AB，
∴QH=DN，
则
| 15 |
| 4 |
| 3 |
| 5 |
解得t=
| 96 |
| 41 |
故t值为
| 96 |
| 41 |
点评：此题考查了相似形综合题，涉及的知识点有矩形的性质，勾股定理，相似三角形的判定与性质等知识．此题综合性很强，难度较大，注意掌握数形结合思想、分类讨论思想与方程思想的应用是解此题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
（2013•莆田质检）如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC于点D，点E是AB上一点，以AE为直径的⊙O过点D，且交AC于点F．
如图，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，AD和BD分别是∠BAC和∠ABC的平分线，它们相交于点D，求点D到BC的距离．
边上移动，使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F，且使DE始终与AB垂直．
如图，在Rt△ABC中，BD⊥AC，sinA=
点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t（s）．