题目内容
 已知:如图,四边形ABCD是关于坐标原点中心对称的四边形,其中点A(1,3),B(3,1),反比例函数=
已知:如图,四边形ABCD是关于坐标原点中心对称的四边形,其中点A(1,3),B(3,1),反比例函数=| k |
| x |
(1)求反比例函数的解析式.
(2)设直线y=ax+b经过C、D两点,在原有坐标系中画出并利用函数的图象,直接写出不等式
| k |
| x |
x<-3或-1<x<0
x<-3或-1<x<0
.分析:(1)把点A坐标代入y=
可求出k,从而得到反比例函数解析式;
(2)利用中心对称得性质确定C点坐标为(-1,-3),D点坐标为(-3,-1),则可判断C(-1,-3)、D(-3,-1)都在反比例函数y=
得图象上,然后观察函数图象得到当x<-3或-1<x<0时,一次函数图象都在反比例函数图象上方,由此可得到不等式
<ax+b的解集.
| k |
| x |
(2)利用中心对称得性质确定C点坐标为(-1,-3),D点坐标为(-3,-1),则可判断C(-1,-3)、D(-3,-1)都在反比例函数y=
| 3 |
| x |
| k |
| x |
解答:解:(1)把A(1,3)代入y=
得k=1×3=3,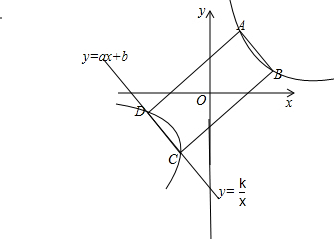
故反比例函数的解析式为y=
;
(2)∵四边形ABCD是关于坐标原点中心对称的四边形,
∴C点坐标为(-1,-3),D点坐标为(-3,-1),
∵-1×(-3)=3,-3×(-1)=3,
∴C(-1,-3)、D(-3,-1)都在反比例函数y=
得图象上,
∴C(-1,-3)、D(-3,-1)为直线y=ax+b与双曲线y=
的交点,
∴当x<-3或-1<x<0时,
<ax+b.
故答案为x<-3或-1<x<0.
| k |
| x |

故反比例函数的解析式为y=
| 3 |
| x |
(2)∵四边形ABCD是关于坐标原点中心对称的四边形,
∴C点坐标为(-1,-3),D点坐标为(-3,-1),
∵-1×(-3)=3,-3×(-1)=3,
∴C(-1,-3)、D(-3,-1)都在反比例函数y=
| 3 |
| x |
∴C(-1,-3)、D(-3,-1)为直线y=ax+b与双曲线y=
| 3 |
| x |
∴当x<-3或-1<x<0时,
| k |
| x |
故答案为x<-3或-1<x<0.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数图象与一次函数图象的交点坐标满足两函数解析式,即求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.

练习册系列答案
相关题目
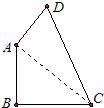 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.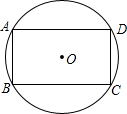 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.